Odejmowanie ułamków
Jak się odejmuje ułamki? Gdy ich mianowniki są takie same, odejmowanie jest proste. Jeżeli jednak mianowniki odejmowanych ułamków różnią się, musimy je sprowadzić do wspólnego mianownika lub zwyczajnie zastosować wzór. Dodawanie i odejmowanie ułamków zwykłych podlega podobnym zasadom.
Odejmowanie ułamków zwykłych o jednakowych mianownikach
Przykłady
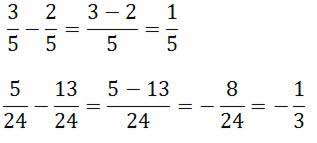
Odejmowanie ułamków o różnych mianownikach
Najprostszym sposobem jest zastosowanie poniższego wzoru:
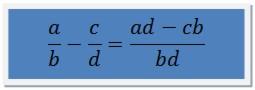
Przykłady
A oto dwa przykłady zastosowania powyższego wzoru:
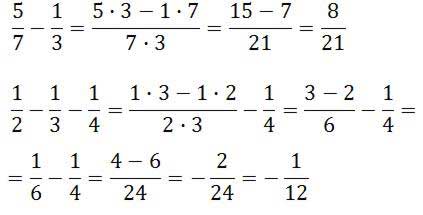
Kalkulator

Odejmowanie ułamków zwykłych
W tym miejscu możesz zobaczyć, w jaki sposób odejmujemy ułamki zwykłe. Nasz robot rozwiązuje dowolne zadanie z tego zakresu.
Wpisz dane:| - | ||||
Zobacz także artykuł dodawanie ułamków zwykłych, w którym również znajdziesz kalkulator i kolejne przykłady działań na ułamkach zwykłych.
Odejmowanie ułamków dziesiętnych omawiamy w artykule o odejmowaniu pisemnym liczb.
Dodawanie, jak i odejmowanie ułamków to umiejętności podstawowe, które należy posiąść, aby radzić sobie z matematyką na kolejnych szczeblach edukacji. Wiele osób ma problemy z odejmowaniem ułamków, szczególnie tych o różnych mianownikach. A wystarczy tylko trochę ćwiczeń, aby nabyć tę umiejętność na bardzo długo.
Zadania z rozwiązaniami

Zadanie nr 1.
Oblicz:
a) \(\frac{1}{8}-\frac{2}{3}\)
b) \(\frac{5}{11}-\frac{3}{7}\)
c) \(\frac{2}{5}-\frac{3}{10}-\frac{1}{4}-\frac{7}{20}\)

Zadanie nr 2.
Oblicz:
a) \(\frac{ab}{c}-\frac{ac}{b}\)
b) \(\frac{5}{1-a}-\frac{a}{2+a}\)
c) \(\frac{1}{2}-\frac{1}{3}-3-\frac{a}{4}\)

Zadanie nr 3 — maturalne.
Różnica \(0,(3)-\frac{23}{33}\) jest równa
A. \(-0,(39)\)
B. \(-\frac{39}{100}\)
C. \(-0,36\)
D. \(-\frac{4}{11}\)
Wybrane karty pracy
Powiązane materiały
 Odejmowanie ułamków zwykłych
Odejmowanie ułamków zwykłych© medianauka.pl, 2008-12-08, A-119
Data aktualizacji artykułu: 2023-03-01

 Odejmowanie
Odejmowanie Odejmowanie pisemne liczb
Odejmowanie pisemne liczb Odejmowanie
Odejmowanie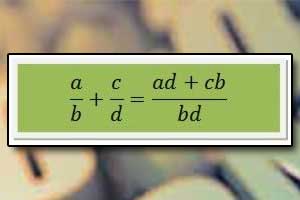 Dodawanie ułamków
Dodawanie ułamków Odejmowanie ułamków zwykłych — quiz
Odejmowanie ułamków zwykłych — quiz Odejmowanie ułamków dziesiętnych
Odejmowanie ułamków dziesiętnych