Liczby zespolone

Czy istnieją liczby inne niż rzeczywiste? Aż trudno uwierzyć, że odpowiedź jest twierdząca! Są to tak zwane liczby zespolone, tworzące zbór liczb zespolonych.

Trochę historii

Już Heron z Aleksandrii w roku około 10-80 użył następującego zapisu pierwiastka z liczby ujemnej:

\(\sqrt{(81-144)}\).

W latach 200-284 Diofantos zapisał liczbę \(\sqrt{(1849-2016)}\) jako możliwy wynik równania kwadratowego.

Pierwszym matematykiem, który zapisał wzór wykorzystujący pierwiastek z liczby ujemnej, był Gerolamo Cardano. Rozważał następujący problem: Jak podzielić liczbę 10 na dwie części, aby ich iloczyn wyniósł 40. Nie da się? Gdy zapiszemy układ równań:

\(\begin{cases} x+y=10\\xy=40\end{cases}\)

otrzymamy rozwiązanie:

\(x=5+\sqrt{-15}\)

\(y=5-\sqrt{-15}\)

Mimo iż w zbiorze liczb rzeczywistych pierwiastek z liczby ujemnej nie istnieje, to zauważmy, że:

\((5+\sqrt{-15})(5-\sqrt{-15})=5^2-(\sqrt{-15})^2=25-(-15)=40\)

Działanie daje nam poprawny wynik, mimo że używamy „dziwnego” pierwiastka w rachunkach!

W 1777 roku Euler oznaczył pierwiastek kwadratowy z wartości ujemnej przez „\(i\)” od słowa łacińskiego imaginarius, co znaczy „urojony”.

Liczby urojone

Jednostka urojona jest to liczba, której kwadrat jest równy -1.

\(i^2=-1\)

Zauważ, że jednostka urojona to nic innego jak \(i=\sqrt{-1}\).

Jednostka urojona posłuży nam do określenia algebraicznej postaci liczby zespolonej.

Postać algebraiczna liczby zespolonej

Liczba zespolona \(z\) jest to suma liczby rzeczywistej i urojonej:

\(z=a+ib\)

gdzie:

\(a, b\) - liczby rzeczywiste;

\(i\) - jednostka urojona.

Liczbę a nazywamy częścią rzeczywistą \(a=Re(z)\) liczby zespolonej, natomiast liczbę b nazywamy częścią urojoną liczby z: \(b=Im(z)\).

Zauważmy, że gdy \(b=0\), to \(z=a\). Oznacza to, że liczby rzeczywiste są szczególnymi przypadkami liczb zespolonych.

Liczba urojona jest to liczba w postaci \(z=0+ib\).

Zbiór liczb zespolonych oznaczamy symbolem \(\mathbb{C}\).

Równość liczb zespolonych

Dwie liczby zespolone są sobie równe, jeśli ich części rzeczywiste i urojone są sobie odpowiednio równe.

Nie rozpatrujemy zaś relacji „mniejsza” i „większa” dla liczb urojonych.

Postać trygonometryczna i wykładnicza liczb zespolonych

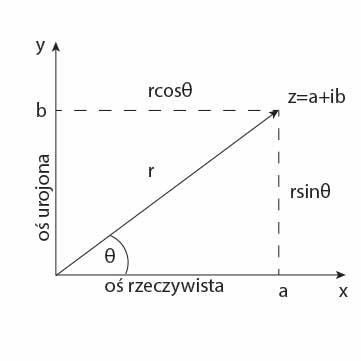
W układzie biegunowym możemy wyrazić liczby zespolone w następujący sposób:

\(z=re^{i\theta}=r(cos\theta+isin\theta)\)

gdzie\(r\) jest to tak zwany moduł liczby zespolonej, oznaczany przez \(|z|\).

Jaki jest związek pomiędzy a, b, r, θ?

Oto przydatne wzory:

\(a=rcos\theta\)

\(b=rsin\theta\)

\(r=\sqrt{a^2+b^2}\)

Przykład

Przykład tej samej liczby zespolonej w różnych reprezentacjach:

postać algebraiczna: \(z=3+i\sqrt{3}\)
postać trygonometryczna: \(z=2(cos{\frac{\pi}{3}}+isin{\frac{\pi}{3}})\)
postać wykładnicza: \(z=2e^{i\frac{\pi}{3}}\)

Moduł liczby zespolonej \(|z|=\sqrt{1^2+\sqrt{3}^2}=\sqrt{1+3}=\sqrt{4}=2\).

Interpretacja geometryczna liczb zespolonych

Liczby rzeczywiste przedstawiamy na osi liczbowej. Liczby zespolone możemy przedstawić na płaszczyźnie, gdzie x jest osią rzeczywistą, natomiast y jest osią urojoną.

interpretacja geometryczna liczb zespolonych

Liczby zespolone sprzężone

Dwie liczby z i z^* są sprzężone, jeżeli ich części rzeczywiste są równe, a części urojone różnią się znakiem. To punkty symetryczne względem osi rzeczywistej.

Interesujący jest poniższy wzór:

\(zz^* = r^2\)

Czasem wydziela się pewną klasę liczb zespolonych, dla których \(zz^* = 1\). Są to tak zwane czynniki fazowe.

Kalkulator liczb zespolonych

Za pomocą tego kalkulatora można wykonać dodawanie, odejmowanie, mnożenie oraz dzielenie liczb zespolonych. Kalkulator pokazuje kolejne kroki poszczególnych działań.

Kalkulator
Działania na liczbach zespolonych

Wpisz dane:

Działanie:

Liczba 1: i +

Liczba 2: i +

Dokładność: miejsc po przecinku.

Rozwiązanie:

Dodajemy do siebie części urojone i rzeczywiste liczb. Otrzymujemy:

equation

Odejmujemy od siebie części urojone i rzeczywiste liczb. Otrzymujemy:

equation

Wymnażamy poszczególne elementy nawiasów i otrzymujemy:

equation

Mnożymy licznik i mianownik przez sprzężenie mianownika i obliczamy:

equation

Objaśnienia:

Jeżeli wynik wskaże wartość „infinity” to oznacza, że jest poza zakresem dostępnym dla niniejszego kalkulatora.
Zapis wyniku 1.2e+12 oznacza liczbę 1.2 pomnożoną przez 10¹².
Gdy jedna z liczb będąca wynikiem działań jest większa od jej reprezentacji 64-bitowej, kalkulator stosuje przybliżenia wyniku.
Jeżeli podasz liczbę rzeczywistą, do obliczeń zostanie wzięta jedynie jej część całkowita.

Oprogramowanie kalkulatora: Natalia Okoń

Czy liczby zespolone się do czegoś przydają?

Ależ tak! Niemalże od razu liczby te znalazły zastosowanie w fizyce, w elektronice w teorii prądu przemiennego, gdzie liczby te okazały się bardzo użyteczne w rachunkach. W fizyce liczby te występują przy opisie fal elektromagnetycznych, do opisu drgań sinusoidalnych. W mechanice kwantowej funkcja falowa, a więc podstawowe pojęcie tej dziedziny nauki, jest funkcją zespoloną! Liczby zespolone odgrywają ogromną rolę w algebrze i geometrii.

Pytania

Czy istnieją liczby rozszerzające ciało liczb zespolonych?

Tak. To kwaterniony, wprowadzone przez W. Hamiltona w 1843 roku. Kwaterniony służą do opisu mechaniki w przestrzeni trójwymiarowej.

Powiązane quizy

Liczby — quiz

Liczba pytań: 21
Quiz szkolny
Średni wynik:
7 pkt / 33.33%
2024-02-18

Inne zagadnienia z tej lekcji

Liczby rzeczywiste