Zadania — inne funkcje
Znajdziesz tutaj zadania z pozostałych funkcji takich, jak wykładnicza, potęgowa, wymierna, homograficzna i logarytmiczna. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 4.
Wyznaczyć dziedzinę funkcji \(y=\log_{\frac{1}{2}}{\frac{x}{x+2}}\).
Zadanie nr 5.
Wyznaczyć dziedzinę funkcji \(y=\log_{(-x^2+2x)}{(x^3-x^2)}\).
Zadanie nr 6.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{3}}{(x-3)}+1\).
Zadanie nr 8.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\).
Zadanie nr 13.
Wykazać, że ciąg \(a_n=(\sqrt{2})^n\) jest ciągiem geometrycznym.
Zadanie nr 14.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{3x^2-2x+1}{2x^3-3x^2-2x}\).
Zadanie nr 15.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{x^4-x^3+x^2+6x-1}{6x^3-5x^2-2x+1}\)
Zadanie nr 16 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej f(x), której dziedziną jest zbiór \(D=(-\infty,3)\cup (3,+\infty)\).
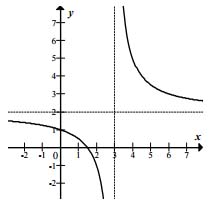
Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
A. w dwóch przypadkach: \(p=0\) lub \(p=3\).
B. w dwóch przypadkach: \(p=0\) lub \(p=2\).
C. tylko wtedy, gdy \(p=3\).
D. tylko wtedy, gdy \(p=2\).
Zadanie nr 17 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do tego wykresu funkcji.
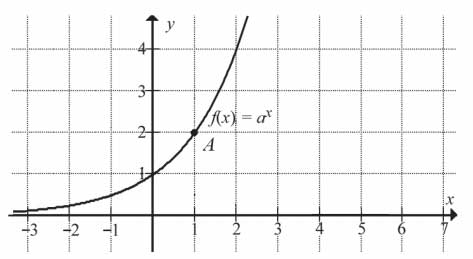
Podstawa potęgi \(a\) jest równa:
A. \(-\frac{1}{2}\)
B. \(1\frac{1}{2}\)
C. -2
D. 2
Zadanie nr 18 - maturalne.
Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=a^x\) (gdzie \(a>0\) i \(a\neq 1\), należy punkt \(P=(2,9)\). Oblicz a i zapisz zbiór wartości funkcji g, określonej wzorem \(g(x)=f(x)−2\).
Liczba odnalezionych zadań w zbiorze: 18.
Oznaczenia
Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom rozszerzony.
