Zadania — funkcja liniowa
Znajdziesz tutaj zadania z funkcji liniowej, jej własności, wykresu funkcji liniowej. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 2.
Średnio tygodniowo autor pewnego bloga zarabia na wyświetlaniu reklam na swojej stronie 20 zł. Jakiego zysku może się spodziewać po roku prowadzenia strony?
Zadanie nr 3.
Babcia w ciągu godziny potrafi wydziergać 20 cm szalika. Ile czasu potrwa wydzierganie całego szalika o długości półtora metra?
Zadanie nr 4.
Sekretarka potrafi napisać średnio 50 słów w ciągu jednej minuty na komputerze. Jak długo potrwa ręczne przepisanie książki o objętości 240 stron, jeżeli wiadomo, że średnio jedna strona maszynopisu zawiera 250 słów, a sekretarka jest jednego dnia w stanie pisać bez przerwy przez 5 godzin?
Zadanie nr 5.
Śnieg padał jednostajnie przez 6,5 h. Spadło 19,5 cm śniegu. Ile śniegu spadło w ciągu jednej godziny?
Zadanie nr 6.
Jeden pracownik składa 500 długopisów w ciągu ośmiu godzin pracy. Ilu pracowników trzeba zatrudnić, aby wykonać zlecenie złożenia 10 000 długopisów w ciągu pięciu dni?
Zadanie nr 7.
Wykres ilustruje zależność zaoszczędzonych środków na lokacie od czasu oszczędzania.
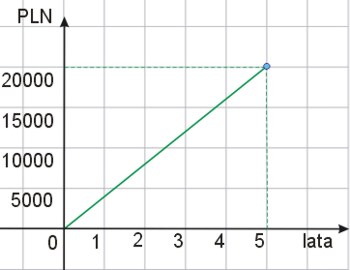
Ile pieniędzy zaoszczędzono po 3 latach oszczędzania?
Zadanie nr 8.
Podczas ostatniego tankowania kierowca wyzerował licznik, przejechał 654 kilometry i zatankował do pełna. Do baku zmieściło się 34,5 l benzyny. Ile litrów na sto kilometrów spala silnik tego samochodu?
Zadanie nr 10.
Naszkicować wykres funkcji \(y=-\sqrt{2}x+1\).Zadanie nr 11.
Naszkicować wykres funkcji \(y=-5x+\frac{1}{2}\), określić jej monotoniczność oraz znaleźć miejsce zerowe.
Zadanie nr 12.
Dana jest prosta o równaniu \(y=-7x+5\). Znaleźć równanie prostej równoległej do tej prostej, przechodzącej przez początek układu współrzędnych.
Zadanie nr 13.
Dana jest prosta o równaniu \(y=5x+\frac{1}{5}\). Znaleźć równanie prostej prostopadłej do tej prostej, przechodzącej przez punkt \(A(1,-1)\).
Zadanie nr 14.
Znaleźć równania prostych zawierających boki kwadratu ABCD, jeśli wiadomo, że współrzędne wierzchołków są liczbami całkowitymi.
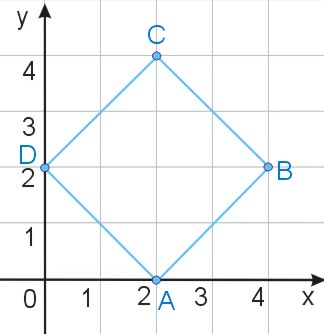
Zadanie nr 15.
Znaleźć równania wszystkich prostych prostopadłych przechodzących przez punkty \(A(1,2), B(2,-1), C(-1,3)\).
Zadanie nr 16.
Znaleźć równanie prostej, która zawiera wysokość w trójkącie \(ABC\) przedstawionym na poniższym rysunku:
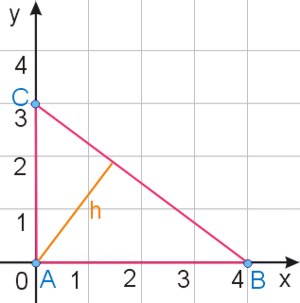

Zadanie nr 17 - maturalne.
Dana jest funkcja liniowa \(f(x)=\frac{3}{4}x+6\). Miejscem zerowym tej funkcji jest liczba:
A. \(8\)
B. \(6\)
C. \(-6\)
D. \(-8\)

Zadanie nr 18 - maturalne.
Proste opisane równaniami \(y=\frac{2}{m-1}x+m-2\) oraz \(y=mx+\frac{1}{m+1}\) są prostopadłe, gdy:
A. \(m=2\)
B. \(m=\frac{1}{2}\)
C. \(m=\frac{1}{3}\)
D. \(m=-2\)

Zadanie nr 19 - maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.

Zadanie nr 20 - maturalne.
Na wykresie funkcji liniowej określonej wzorem \(f(x)=(m-1)x+3\) leży punkt \(S=(5,-2)\). Zatem:
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=2\)

Zadanie nr 21 - maturalne.
Funkcja liniowa f określona wzorem \(f(x)=2x+b\) ma takie samo miejsce zerowe, jakie ma funkcja liniowa \(g(x)=-3x+4\). Stąd wynika, że
A. \(b=4\)
B. \(b=-\frac{3}{2}\)
C. \(b=-\frac{8}{3}\)
D. \(b=\frac{4}{3}\)

Zadanie nr 22 - maturalne.
Prosta l o równaniu \(y=m^2x+3\) jest równoległa do prostej k o równaniu \(y=(4m-4)x-3\). Zatem:
A. \(m=2\)
B. \(m=-2\)
C. \(m=-2-2\sqrt{2}\)
D. \(m=-2+2\sqrt{2}\)

Zadanie nr 23 - maturalne.
Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla:
A. \(m=-\frac{1}{2}\)
B. \(m=\frac{1}{2}\)
C. \(m=1\)
D. \(m=2\)

Zadanie nr 24 - maturalne.
W układzie współrzędnych są dane punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta AB przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

Zadanie nr 25 - maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)

Zadanie nr 26 - maturalne.
Funkcja liniowa \(f(x)=(m^2-4)x+2\) jest malejąca, gdy:
A. \(m\in [-2,2]\)
B. \(m\in (-2,2)\)
C. \(m\in (-\infty,2]\)
D. \(m\in [2,+\infty)\)

Zadanie nr 27 - maturalne.
O funkcji liniowej \(f\) wiadomo, że \(f(1)=2\). Do wykresu tej funkcji należy punkt \(P=(-2,3)\). Wzór funkcji \(f\) to:
A. \(f(x)=-\frac{1}{3}x+7/3\)
B. \(f(x)=-\frac{1}{2}x+2\)
C. \(f(x)=-3x+7\)
D. \(f(x)=-2x+4\)

Zadanie nr 28 - maturalne.
Na rysunku przedstawiona jest prosta \(k\), przechodząca przez punkt \(A=(2,-3)\) i przez początek układu współrzędnych oraz zaznaczony jest kąt \(\alpha\) nachylenia tej prostej do osi \(Ox\).
A. \(tg\alpha = -\frac{2}{3}\)
B. \(tg\alpha = -\frac{3}{2}\)
C. \(tg\alpha = \frac{2}{3}\)
D. \(tg\alpha = \frac{3}{2}\)
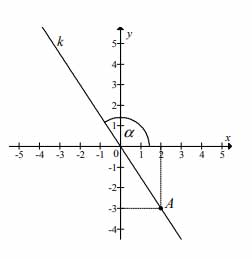

Zadanie nr 29 - maturalne.
Na płaszczyźnie z układem współrzędnych proste k i l przecinają się pod kątem prostym w punkcie A = (-2, 4). Prosta k jest określona równaniem \(y=-\frac{1}{4}x+\frac{7}{2}\). Zatem prostą l opisuje równanie
A. \(y=\frac{1}{4}x + \frac{7}{2}\)
B. \(y=-\frac{1}{4}x + \frac{7}{2}\)
C. \(y=4x-12\)
D. \(y=4x+12\)

Zadanie nr 30 - maturalne.
Funkcja liniowa \(f\) określona jest wzorem \(f(x)=\frac{1}{3}x-1\), dla wszystkich liczb rzeczywistych \(x\). Wskaż zdanie prawdziwe.
- Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,\frac{1}{3})\).
- Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,-1)\).
- Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,\frac{1}{3})\).
- Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P=(0,-1)\).

Zadanie nr 31 - maturalne.
Liczba \(1\) jest miejscem zerowym funkcji liniowej \(f(x)=ax+b\), a punkt \(M=(3,−2)\) należy do wykresu tej funkcji. Współczynnik \(a\) we wzorze tej funkcji jest równy
- \(1\)
- \(\frac{3}{2}\)
- \(-\frac{3}{2}\)
- \(-1\)

Zadanie nr 32 - maturalne.
W układzie współrzędnych punkty \(A=(4,3)\) i \(B=(10,5)\) są wierzchołkami trójkąta ABC. Wierzchołek \(C\) leży na prostej o równaniu \(y=2x+3\). Oblicz współrzędne punktu \(C\), dla którego kąt \(ABC\) jest prosty.

Zadanie nr 33 - maturalne.
Proste o równaniach \(y=(2m+2)x−2019\) oraz \(y=(3m−3)x+2019\) są równoległe, gdy
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=5\)

Zadanie nr 34 - maturalne.
Prosta o równaniu \(y=ax+b\) jest prostopadła do prostej o równaniu \(y=− 4x+1\) i przechodzi przez punkt \(P=(\frac{1}{2},0)\), gdy
A. \(a=-4\) i \(b=-2\)
B. \(a=\frac{1}{4}\) i \(b=-\frac{1}{8}\)
C. \(a=-4\) i \(b=2\)
D. \(a=\frac{1}{4}\) i \(b=\frac{1}{2}\)

Zadanie nr 35 - maturalne.
Funkcja \(f\) jest określona dla każdej liczby rzeczywistej \(x\neq −2\) wzorem:
\(f(x)=\frac{|x+2|}{x+2}-x+3|x-1|\)
Wyznacz zbiór wartości tej funkcji.

Zadanie nr 36 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=ax+b\).
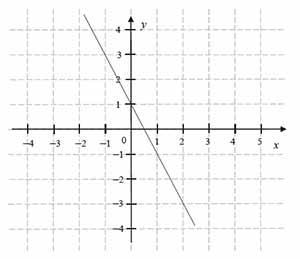
A. \(a+b>0\)
B. \(a+b=0\)
C. \(a\cdot b>0\)
D. \(a\cdot b<0\)

Zadanie nr 37 - maturalne.
Proste o równaniach \(y=(m−2)x\) oraz \(y=\frac{3}{4}x+7\) są równoległe. Wtedy
A. \(m=-\frac{5}{4}\)
B. \(m=\frac{2}{3}\)
C. \(m=\frac{11}{4}\)
D. \(m=\frac{10}{3}\)

Zadanie nr 38 - maturalne.
Prosta przechodząca przez punkty \(A=(3,−2)\) i \(B=(−1,6)\) jest określona równaniem
A. \(y=-2x+4\)
B. \(y=-2x-8\)
C. \(y=2x+8\)
D. \(y=2x-4\)

Zadanie nr 39 - maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
Proste o równaniach \(y=3x-5\) oraz \(y=\frac{(m-3)}{2}+\frac{9}{2}\) są równoległe, gdy
A. \(m=1\)
B. \(m=3\)
C. \(m=6\)
D. \(m=9\)

Zadanie nr 40 - maturalne.
Punkty \(A=(−2,6)\) oraz \(B=(3, b)\) leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy b jest równe
A. 9
B. (-9)
C. (-4)
D. 4

Zadanie nr 41 - maturalne.
Dane są cztery proste k, l, m o równaniach:
\(k: y=-x+1\)
\(l: y=\frac{2}{3}x+1\)
\(m: y=-\frac{3}{2}x+4\)
\(n: y=-\frac{2}{3}x-1\)
Wśród tych prostych prostopadłe są
A. proste k oraz l.
B. proste k oraz n.
C. proste l oraz m.
D. proste m oraz n.

Zadanie nr 42 - maturalne.
Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych \(x,y\) jednego z niżej zapisanych układów równań \(A–D\).
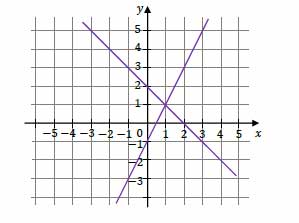
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A. \(\begin{cases} y=-x+2\\y=-2x+1\end{cases}\)
B. \(\begin{cases} y=x-2\\y=-2x-1\end{cases}\)
C. \(\begin{cases} y=x-2\\y=2x+1\end{cases}\)
D. \(\begin{cases} y=-x+2\\y=2x-1\end{cases}\)

Zadanie nr 43 - maturalne.
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji \(f\) w kartezjańskim układzie współrzędnych (x,y).
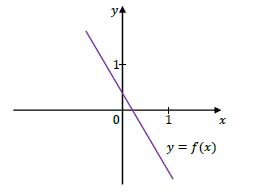
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(a\) oraz liczba \(b\) we wzorze funkcji \(f\) spełniają warunki:
A. \(a>0\) i \(b>0\)
B. \(a>0\) i \(b<0\)
C. \(a<0\) i \(b>0\)
D. \(a<0\) i \(b<0\)

Zadanie nr 44 - maturalne.
W kartezjańskim układzie współrzędnych \(x,y\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O=(0,0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(0x\), a drugie przechodzi przez punkt \(P=(-3,1)\) (zobacz rysunek).
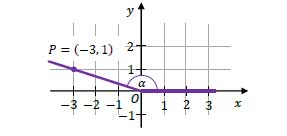
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Tangens kąta \(\alpha\) jest równy
A. \(\frac{1}{\sqrt{10}}\)
B. \((-\frac{3}{\sqrt{10}})\)
C. \((-\frac{3}{1})\)
D. \((-\frac{1}{3})\)

Zadanie nr 45 - maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) dana jest prosta \(k\) o równaniu \(y=-\frac{1}{3}x+2\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Prosta o równaniu \(y=ax+b\) jest równoległa do prostej \(k\) i przechodzi przez punkt \(P=(3,5)\), gdy
A. \(a=3, b=4\)
B. \(a=-\frac{1}{3}, b=4\)
C. \(a=3, b=-4\)
D. \(a=-\frac{1}{3}, b=6\)
Liczba odnalezionych zadań w zbiorze: 45.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.




