
Zadanie maturalne nr 18, matura 2017 (poziom podstawowy)
Treść zadania:
Na rysunku przedstawiona jest prosta \(k\), przechodząca przez punkt \(A=(2,-3)\) i przez początek układu współrzędnych oraz zaznaczony jest kąt \(\alpha\) nachylenia tej prostej do osi \(Ox\).
A. \(tg\alpha = -\frac{2}{3}\)
B. \(tg\alpha = -\frac{3}{2}\)
C. \(tg\alpha = \frac{2}{3}\)
D. \(tg\alpha = \frac{3}{2}\)
Rozwiązanie zadania
Wykorzystamy równanie prostej postaci \(y=ax+b\). Pamiętamy, że współczynnik \(a\) jest równy \(tg\alpha \), a jako, że prosta przechodzi przez środek układu, to \(b=0\), więc wystarczy podstawić współrzędne punktu do równania \(y=ax\):
\(y=ax\)
\(a=tg\alpha\)
\(-3=2tg\alpha\)
\(tg\alpha = -\frac{3}{2}\)
Odpowiedź
Odpowiedź B© medianauka.pl, 2019-09-17, ZAD-3686


Zadania podobne
Zadanie nr 1.
Naszkicować wykres funkcji \(y=-\sqrt{2}x+1\).Zadanie nr 2.
Naszkicować wykres funkcji \(y=-5x+\frac{1}{2}\), określić jej monotoniczność oraz znaleźć miejsce zerowe.

Zadanie nr 3 — maturalne.
W układzie współrzędnych są dane punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta AB przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

Zadanie nr 4 — maturalne.
Na płaszczyźnie z układem współrzędnych proste k i l przecinają się pod kątem prostym w punkcie A = (-2, 4). Prosta k jest określona równaniem \(y=-\frac{1}{4}x+\frac{7}{2}\). Zatem prostą l opisuje równanie
A. \(y=\frac{1}{4}x + \frac{7}{2}\)
B. \(y=-\frac{1}{4}x + \frac{7}{2}\)
C. \(y=4x-12\)
D. \(y=4x+12\)

Zadanie nr 5 — maturalne.
Prosta przechodząca przez punkty \(A=(3,−2)\) i \(B=(−1,6)\) jest określona równaniem
A. \(y=-2x+4\)
B. \(y=-2x-8\)
C. \(y=2x+8\)
D. \(y=2x-4\)

Zadanie nr 6 — maturalne.
Punkty \(A=(−2,6)\) oraz \(B=(3, b)\) leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy b jest równe
A. 9
B. (-9)
C. (-4)
D. 4

Zadanie nr 7 — maturalne.
Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych \(x,y\) jednego z niżej zapisanych układów równań \(A–D\).
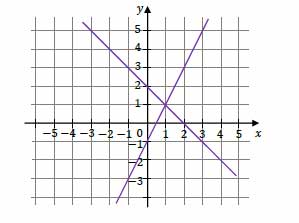
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A. \(\begin{cases} y=-x+2\\y=-2x+1\end{cases}\)
B. \(\begin{cases} y=x-2\\y=-2x-1\end{cases}\)
C. \(\begin{cases} y=x-2\\y=2x+1\end{cases}\)
D. \(\begin{cases} y=-x+2\\y=2x-1\end{cases}\)

Zadanie nr 8 — maturalne.
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji \(f\) w kartezjańskim układzie współrzędnych (x,y).
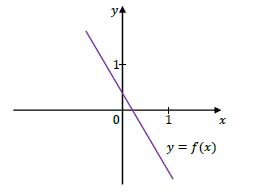
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(a\) oraz liczba \(b\) we wzorze funkcji \(f\) spełniają warunki:
A. \(a>0\) i \(b>0\)
B. \(a>0\) i \(b<0\)
C. \(a<0\) i \(b>0\)
D. \(a<0\) i \(b<0\)

Zadanie nr 9 — maturalne.
W kartezjańskim układzie współrzędnych \(x,y\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O=(0,0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(0x\), a drugie przechodzi przez punkt \(P=(-3,1)\) (zobacz rysunek).
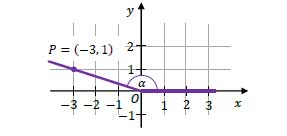
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Tangens kąta \(\alpha\) jest równy
A. \(\frac{1}{\sqrt{10}}\)
B. \((-\frac{3}{\sqrt{10}})\)
C. \((-\frac{3}{1})\)
D. \((-\frac{1}{3})\)

