Wykres funkcji potęgowej

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Wykres funkcji potęgowej zależy od wartości wykładnika. Przeanalizujemy zatem kilka przypadków.

Wykładnik zerowy

Mamy w tym przypadku funkcję \(y=x^0\). Argumentowi \(x=0\) przypisujemy wartość 1. Mamy więc wykres funkcji stałej \(y=1\). Należy pamiętać, że dotyczy to przypadku \(x\neq 0\).

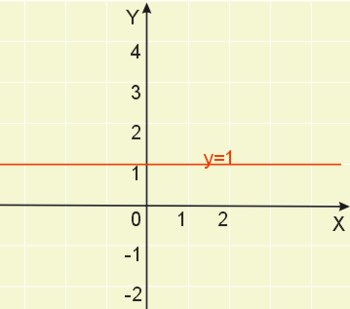
wykres funkcji stałej, potęgowej w przypadku, gdy wykładnik jest równy 0

Wykładnik całkowity dodatni

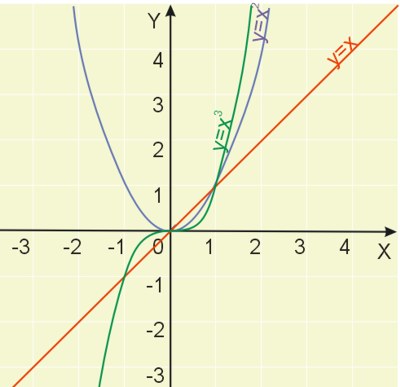
Gdy wykładnik \(a=1\) mamy w tym przypadku funkcję \(y=x\). Mamy więc wykres funkcji liniowej. Wykresem jest więc prosta (kolor czerwony na rysunku).

Gdy wykładnik \(a=2\), mamy do czynienia z funkcją kwadratową, której wykresem jest parabola (kolor niebieski na ilustracji).

Ilustracja przedstawia też wykres funkcji potęgowej o wykładniku \(a=3\) (kolor zielony).

wykres funkcji potęgowej gdy wykładnik jest dodatni

Wykładnik całkowity ujemny

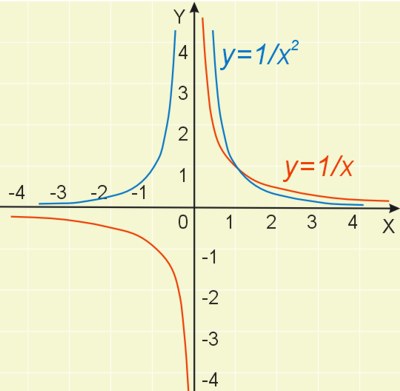
Gdy wykładnik \(a=-1\) mamy w tym przypadku funkcję \(y=x^{-1}=\frac{1}{x}\), której wykresem jest hiperbola (kolor czerwony na rysunku).

Gdy wykładnik \(a=-2\), mamy do czynienia z funkcją \(y=x^{-2}=\frac{1}{x^2}\) (kolor niebieski na ilustracji).

wykres funkcji potęgowej o wykładniku ujemnym

Wykres Wykres funkcji potęgowej online

Poniższa symulacja ilustruje zachowanie wykresu funkcji potęgowej przy zmianie wykładnika.

Funkcja w postaci y = x^a, czyli y = x

a 1

W pozostałych przypadkach warto sporządzić tabelkę wartości funkcji lub skorzystać z analizy funkcji z wykorzystaniem rachunku pochodnych.

Ćwiczenia

Zwiększ populację dziobaków, rozwiązując krótkie zadania i ćwiczenia związane z tą lekcją.

Nie jesteś zalogowany.

Z jajka nic się nie wykluje, a Twoja populacja dziobaków nie przetrwa po opuszczeniu strony... Zaloguj się

Aby otworzyć złote jaja, musisz posiadać Plan Premium.

Powiązane materiały

Funkcja potęgowa