Zadania — funkcja kwadratowa
Znajdziesz tutaj zadania z funkcji kwadratowej, jej własności, wykresu, postaci kanonicznej i iloczynowej. Znajdziesz tu także zadania tekstowe. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 2.
Dla jakiej wartości parametrów \(m\) i \(n\) wierzchołkiem paraboli o równaniu \(y=x^2-mx+n+1\) jest punkt \(A(2,1)\)?
.Zadanie nr 5.
Znaleźć równanie osi symetrii paraboli o równaniu \(f(x)=-2x^2+x-3\).
Zadanie nr 6.
Sporządzić wykres funkcji \(f(x)=\begin{cases}x^2 \ dla \ x<0\\ -x^2\ dla \ x\geq 0\end{cases}\)
Zadanie nr 7.
Znaleźć równanie paraboli, której fragment przedstawiono na rysunku:
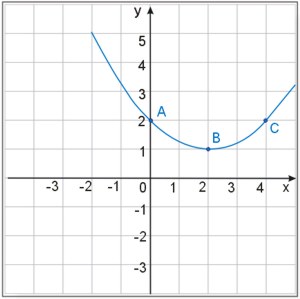
Zadanie nr 8.
Przedstawić funkcję
a) \(f(x)=-x^2+7x-12\)
b) \(f(x)=2x^2+44x+242\)
w postaci iloczynowej.
Zadanie nr 9.
Zapisać wzór funkcji kwadratowej, która ma dwa miejsca zerowe \(x_1=-1\) oraz \(x_2=5\), wiedząc że parabola przecina oś OY w punkcie (0,15).
Zadanie nr 10.
Sprowadzić do postaci kanonicznej funkcję \(f(x)=2x^2+2x+1\).
Zadanie nr 11.
Wykres funkcji \(y=-x^2\) przesunięto o wektor \(\vec{u}=[-5,5]\). Jakie jest równanie paraboli, powstałej w wyniku przesunięcia?
Zadanie nr 12 - maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).
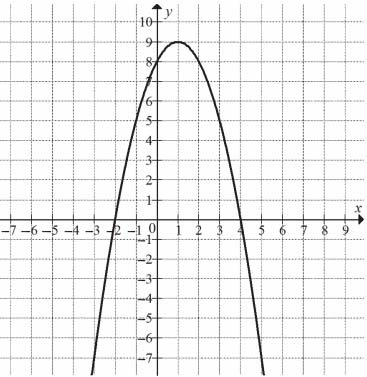
Zbiorem wartości funkcji \(f\) jest przedział:
A. \((-\infty,-2]\)
B. \([-2,4]\)
C. \([4,\infty)\)
D. \((-\infty,9]\)
Zadanie nr 13 - maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).
Najmniejsza wartość funkcji \(f\) w przedziale \([−1, 2]\) jest równa
A. \(2\)
B. \(5\)
C. \(8\)
D. \(9\)
Zadanie nr 14 - maturalne.
Funkcja kwadratowa określona jest wzorem \(f(x)=x^2+x+c\). Jeżeli \(f(3)=4\), to:
A. \(f(1)=-6\)
B. \(f(1)=0\)
C. \(f(1)=6\)
D. \(f(1)=18\)
Zadanie nr 15 - maturalne.
Oblicz najmniejszą i największą wartość funkcji kwadratowej \(f(x) = x^2-6x+3\) w przedziale \([0,4]\).
Zadanie nr 16 - maturalne.
Liczby \((-1)\) i \(3\) są miejscami zerowymi funkcji kwadratowej \(f\). Oblicz \(\frac{f(6)}{f(12)}\).
Zadanie nr 17 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\).
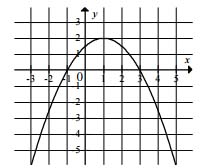
Funkcja \(f\) jest określona wzorem
A. \(f(x)=\frac{1}{2}(x+3)(x-1)\)
B. \(f(x)=\frac{1}{2}(x-3)(x+1)\)
C. \(f(x)=-\frac{1}{2}(x+3)(x-1)\)
D. \(f(x)=-\frac{1}{2}(x-3)(x+1)\)
Zadanie nr 18 - maturalne.
Pierwiastki \(x_1\), \(x_2\) równania \(2(x+2)(x-2)=0\) spełniają warunek:
A. \(\frac{1}{x_1}+\frac{1}{x_2}=-1\)
B. \(\frac{1}{x_1}+\frac{1}{x_2}=0\)
C. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{4}\)
D. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}\)
Zadanie nr 19 - maturalne.
Wykresem funkcji kwadratowej \(f(x)=2x^2+bx+c\) jest parabola, której wierzchołkiem jest punkt \(W=(4,0)\). Oblicz wartości współczynników \(b\) i \(c\).
Zadanie nr 20 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f(x)=ax^2+bx +c\), której miejsca zerowe to: −3 i 1.
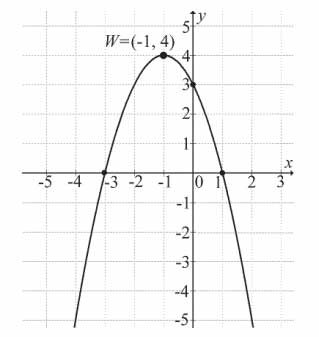
Współczynnik c we wzorze funkcji f jest równy:
A. 1
B. 2
C. 3
D. 4
Zadanie nr 21 - maturalne.
Funkcja kwadratowa określona jest wzorem \(f(x)=-2(x+3)(x-5)\). Liczby \(x_1, x_2\) są różnymi miejscami zerowymi funkcji \(f\). Zatem
- \(x_1+x_2=-8\)
- \(x_1+x_2=-2\)
- \(x_1+x_2=2\)
- \(x_1+x_2=8\)
Zadanie nr 22 - maturalne.
Wykresem funkcji kwadratowej \(f(x)=x^2−6x−3\) jest parabola, której wierzchołkiem jest punkt o współrzędnych
- \((-6,-3)\)
- \((-6,69)\)
- \((3,-12)\)
- \((6,-3)\)
Zadanie nr 23 - maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(2,− 4)\). Liczby \(0\) i \(4\) to miejsca zerowe funkcji \(f\).
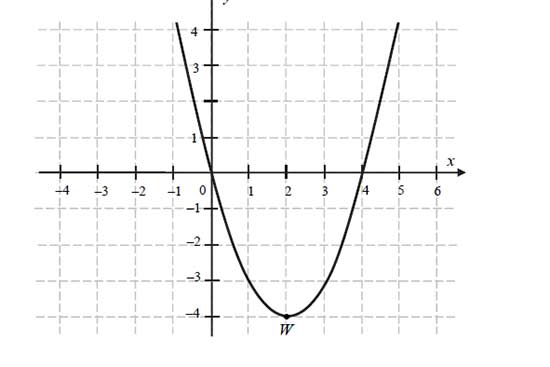
Zadanie 8: Zbiorem wartości funkcji \(f\) jest przedział
A. \((-\infty ,0\rangle \)
B. \(\langle 0, 4\rangle \)
C. \(\langle -4, +\infty)\)
D. \(\langle 4, +\infty)\)
Zadanie 9: Największa wartość funkcji \(f\) w przedziale \(\langle 1, 4\rangle \) jest równa
A. \(-3\)
B. \(-4\)
C. \(4\)
D. \(0\)
Zadanie 10: Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu
A. \(x=-4\)
B. \(x=-4\)
C. \(y=2\)
D. \(x=2\)
Zadanie nr 24 - maturalne.
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=a(x−1)(x−3)\). Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt \(W=(2,1)\).
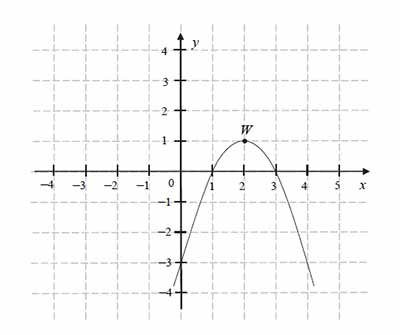
Współczynnik a we wzorze funkcji \(f\) jest równy
A. \(1\)
B. \(2\)
C. \(-2\)
D. \(-1\)
Największa wartość funkcji \(f\) w przedziale \(\langle 1, 4\rangle \) jest równa
A. \(-3\)
B. \(0\)
C. \(1\)
D. \(2\)
Osią symetrii paraboli będącej wykresem funkcji \(f\) jest prosta o równaniu
A. \(x=1\)
B. \(x=2\)
C. \(y=1\)
D. \(y=2\)
Zadanie nr 25 - maturalne.
Funkcja kwadratowa \(f\) określona wzorem \(f(x)=-2(x+1)(x-3)\) jest malejąca w przedziale
A. \([1, +\infty)\)
B. \((−\infty, 1]\)
C. \((−\infty, −8]\)
D. \([−8, +\infty)\)
Zadanie nr 26 - maturalne.
Wykresem funkcji kwadratowej \(f(x)=3x^2+bx+c\) jest parabola o wierzchołku w punkcie \(W=(−3,2)\). Wzór tej funkcji w postaci kanonicznej to
A. \(f(x)=3(x-3)^2+2\)
B. \(f(x)=3(x+3)^2+2\)
C. \(f(x)=(x-3)^2+2\)
D. \(f(x)=(x+3)^2+2\)
Zadanie nr 27.
Piąty wyraz ciągu geometrycznego jest równy \(\frac{1}{\sqrt{2}}\), a siódmy \(\sqrt{2}\). Znaleźć dziewiąty wyraz ciągu i obliczyć sumę pierwszych dziesięciu wyrazów tego ciągu geometrycznego.
Zadanie nr 28 - maturalne.
Jednym z miejsc zerowych funkcji kwadratowej \(f\) jest liczba \((−5)\). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji \(f\), jest równa \(3\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Drugim miejscem zerowym funkcji \(f\) jest liczba
A. 11
B. 1
C. (-1)
D. (-13)
Liczba odnalezionych zadań w zbiorze: 28.
Oznaczenia
Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom rozszerzony.
