Wariancja i odchylenie standardowe

Wariancja \(\sigma^2\) zestawu liczb \(x_1,x_2,...,x_k\), z których \(x_1\) powtarza się \(n_1\) razy, ..., \(x_k\) powtarza się \(n_k\) razy, jest to liczba określona wzorem:

\(\sigma^2=\frac{n_1(x_1-\overline{x})^2+n_2(x_2-\overline{x})^2+...+n_k(x_k-\overline{x})^2}{n}\)

Można dla ułatwienia stosować także wzór:

\(\sigma^2=\frac{n_1x_1^2+n_2x_2^2+...+n_kx_k^2}{n}-\overline{x}^2\)

Wariancja jest miarą rozproszenia danych w kwadratach jednostek, w których dokonujemy pomiaru. Aby stosować tę samą jednostkę dla badania rozproszenia, stosujemy pojęcie odchylenia standardowego, które obliczamy ze wzoru:

\(\sigma=\sqrt{\sigma^2}\)

Zadania z rozwiązaniami

Zadanie nr 1.

W pewnej populacji rodzin wykonano ankietę badającą miesięczne średnie wydatki rodziny na kulturę. Wyniki przedstawia tabela:

Średnia wysokość wydatku na kulturę	Liczba rodzin
0 zł	2
50 zł	15
100 zł	158
150 zł	52
200 zł	48
250 zł	12
300 zł	3

a) Oblicz ile średnio ankietowana rodzina wydaje pieniędzy w ciągu miesiąca na kulturę.

b) Wyznacz medianę miesięcznych wydatków na kulturę.

c) Oblicz wariancję i odchylenie standardowe miesięcznych wydatków na kulturę.

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

W zestawie \(2, 2, 2, ..., 2, 4, 4, 4, ..., 4\) liczb jest \(2m\) liczb (\(m\geq 1\)) , w tym \(m\) liczb \(2\) i \(m\) liczb \(4\). Odchylenie standardowe tego zestawu liczb jest równe

A. \(2\)

B. \(1\)

C. \(\frac{1}{\sqrt{2}}\)

D. \(\sqrt{2}\)

Pokaż rozwiązanie zadania.

Powiązane materiały

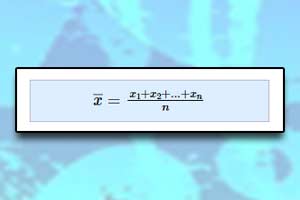Średnia arytmetyczna

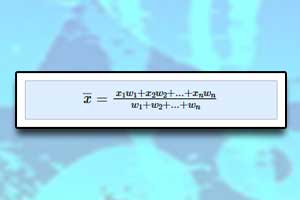Średnia ważona

Mediana

Pojęcia podstawowe statystyki