Mediana
Co to jest mediana? Jak obliczyć medianę? Zacznijmy od definicji.
Mediana (wartość środkowa) zestawu niemalejących danych statystycznych (liczb rzeczywistych) \(x_1,x_2,...,x_n\) jest to liczba \(M\), która dzieli ten zestaw liczb na dwie części o równej liczebności i określona jest wzorem:
Mediana dzieli zestaw danych na dwie części, jedną zawierającą dane nie większe, a druga — nie mniejsze od mediany.
Powyższy wzór na medianę zastosujemy na przykładzie.
Przykład 1
Dla ciągu liczb \((1,2,3,4,5)\), liczba \(3\) jest medianą tego ciągu.
Przykład 2
Dany jest zestaw liczb: \(5,8,5,6,2,1,8,9\). Wyznaczyć medianę tego zestawu.
Najpierw musimy uporządkować zestaw niemalejąco: \(1,2,5,5,6,8,8,9\).
Liczba danych \(n=8\) i jest liczbą parzystą. Stosujemy drugi wzór.
\(M=\frac{1}{2}(x_{\frac{n}{2}}+x_{\frac{n}{2}+1}) =\)
=\(\frac{1}{2}(x_{\frac{8}{2}}+x_{\frac{8}{2}+1}) =\)
\(=\frac{1}{2}(x_4+x_{5}) = \frac{1}{2}(5+6)=5,5\)
Przykład 3
Mediana uporządkowanego zestawu danych to:
- Dla nieparzystej liczby danych — liczba, która znajduje się w środku zestawu: \(1, 5,\) 8, \(9, 10\), czyli \(8\).
- Dla parzystej liczby danych — średnia arytmetyczna dwóch środkowych liczb w danym zestawie: \(1,5,\) 4, 8, \(9,10\), czyli \(\frac{4+8}{2}=6\).
Pytania
Kiedy mediana ma zastosowanie?
Podamy inny niż wyżej przykład. Załóżmy, że 50 drużyn z Polski walczy w turnieju gier sieciowych i co miesiąc podawane są wyniki punktowe tych drużyn. Gdy obliczymy medianę wyników drużyn, a nasz wynik będzie zbliżony do mediany, to liczba ta nam powie, że mniej więcej tyle samo drużyn nas wyprzedza, co jest za nami. w rankingu.
Jeżeli twoje zarobki w grupie pracowników na tym samym stanowisku pracy jest równa pewnej kwocie, a mediana zarobków jest równa tej kwocie, to znaczy, że tyle samo pracowników zarabia lepiej od ciebie, ile jest osób gorzej zarabiających.
Czy można obliczać medianę z liczb ujemnych i ułamków?
Tak. Stosujemy medianę dla dowolnych liczb rzeczywistych.
Zadania z rozwiązaniami

Zadanie nr 1.
Dany jest zestaw liczb:
a) \(100,55,1,1000,2,333,4,55,2000\).
b) \(0,1,5,11,-4,9,1,-5\).
Wyznaczyć medianę tego zestawu.

Zadanie nr 2 — maturalne.
Średnia arytmetyczna sześciu liczb naturalnych \(31, 16, 25, 29, 27, x\) jest równa \(\frac{x}{2}\). Mediana tych liczb jest równa
A. 26
B. 27
C. 28
D. 29

Zadanie nr 3 — maturalne.
Mediana zestawu danych \(2, 12, a, 10, 5, 3\) jest równa \(7\). Wówczas:
A. \(a=4\)
B. \(a=6\)
C. \(a=7\)
D. \(a=9\)

Zadanie nr 4 — maturalne.
Mediana zestawu sześciu danych liczb \(4, 8, 21, a, 16, 25\) jest równa \(14\). Zatem
A. \(a=7\)
B. \(a=12\)
C. \(a=14\)
D. \(a=20\)

Zadanie nr 5 — maturalne.
Cztery liczby: \(2, 3, a, 8\), tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: \(5, 3, 6, 8, 2\). Zatem
A. \(a=7\)
B. \(a=6\)
C. \(a=5\)
D. \(a=4\)

Zadanie nr 6 — maturalne.
Sześciowyrazowy ciąg liczbowy \((1, 2, 2x, x + 2, 5, 6)\) jest niemalejący. Mediana wyrazów tego ciągu jest równa \(4\). Wynika stąd, że
A. \(x=1\)
B. \(x=\frac{3}{2}\)
C. \(x=2\)
D. \(x=\frac{8}{3}\)

Zadanie nr 7 — maturalne.
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
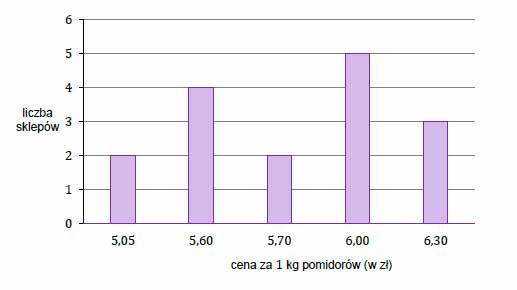
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
| 1. | Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa | |
| 2. | Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa |
A. 5,80 zł
B. 5,73 zł
C. 5,85 zł
D. 6 zł
E. 5,70 zł
Powiązane materiały
© medianauka.pl, 2011-08-13, A-1421
Data aktualizacji artykułu: 2023-07-25

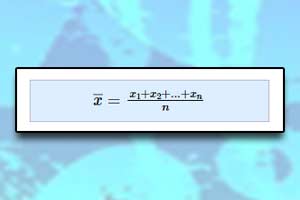 Średnia arytmetyczna
Średnia arytmetyczna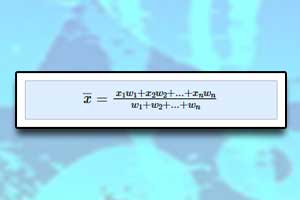 Średnia ważona
Średnia ważona Dominanta
Dominanta Wariancja i odchylenie standardowe
Wariancja i odchylenie standardowe Pojęcia podstawowe statystyki
Pojęcia podstawowe statystyki