Średnia arytmetyczna
Co to jest średnia arytmetyczna? Jak obliczyć średnią arytmetyczną? Zacznijmy od jej definicji.
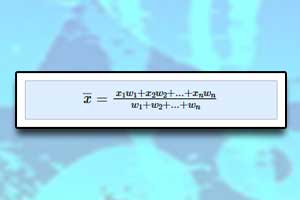
Średnia arytmetyczna liczb rzeczywistych \(x_1,x_2,...,x_n\) jest to liczba \(\overline{x}\) określona wzorem:
Powyższy wzór na średnią arytmetyczną zastosujemy w przykładzie, jak jest wyliczana średnia arytmetyczna ocen szkolnych.
Średniej arytmetycznej używamy wówczas, kiedy opracowując dane statystyczne, chcemy scharakteryzować pewien cały ich zestaw. Średniej arytmetycznej możemy użyć, gdy wszystkie dane mają takie samo znaczenie.
Przykład
Jasiek ma z matematyki następujące oceny: \(3+,2+,5,5,4\). Jakim uczniem jest Jasiek?
To bardzo ogólnie sformułowane zadanie. O tym, czy uczeń jest dobry, bardzo dobry czy słaby w pewnym stopniu decydują oceny. Musimy wystawić uczniowi jedną ocenę, która go scharakteryzuje. Zakładamy, że wszystkie oceny są równie ważne. Obliczymy więc średnią arytmetyczną ocen. Mamy \(5\) ocen, plusy traktujemy jako liczbę \(0,5\).
\(\overline{x}=\frac{3.5+2.5+5+5+4}{5} = \frac{20}{5}=4\)
Możemy śmiało stwierdzić, że Jasiek jest dobrym uczniem.
Gdy w powyższym przykładzie oceny mają różne znaczenie, na przykład \(2+\) Jasiek otrzymał za sprawdzian, a piątki za zadanie domowe, średnia arytmetyczna już gorzej odzwierciedla poziom wiedzy Jaśka. Warto wówczas zastosować tak zwaną średnią ważoną.
Pytania
Jak obliczyć średnią arytmetyczną w programie Excel?
Używamy formuły o nazwie '=ŚREDNIA()'. Jeżeli w komórce A1 wpiszemy liczbę 2, w komórce A2 liczbę 4, natomiast w komórce A3 formułę '=ŚREDNIA(A1;A2)', to po naciśnięciu klawisza ENTER otrzymamy w niej wynik 3.
Nie każdy wie, że jeżeli zaznaczymy kilka komórek, w których znajdują się liczby, to Excel automatycznie pokazuje średnią arytmetyczną tych liczb w prawym dolnym rogu na pasku.
Zadania z rozwiązaniami

Zadanie nr 1.
W zespole pracowników liczącym 30 osób 30% urodziło się w 1971 roku, 20% w 1980, 2 osoby w 1954 roku, 1 osoba w 1990, 3 osoby w 1972, 3 w 1973, 3 w 1975, 2 w 1979, 1 osoba w 1981. Jaka jest średnia wieku w zespole?

Zadanie nr 2.
Oblicz średnią arytmetyczną dziesięciu kolejnych liczb pierwszych.

Zadanie nr 3 — maturalne.
Średnia arytmetyczna sześciu liczb naturalnych \(31, 16, 25, 29, 27, x\) jest równa \(\frac{x}{2}\). Mediana tych liczb jest równa
A. 26
B. 27
C. 28
D. 29

Zadanie nr 4 — maturalne.
W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.

Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.

Zadanie nr 5 — maturalne.
Średnia arytmetyczna zestawu danych: \(2, 4, 7, 8, 9\) jest taka sama jak średnia arytmetyczna zestawu danych: \(2, 4, 7, 8, 9, x\). Wynika stąd, że
A. \(x=0\)
B. \(x=3\)
C. \(x=5\)
D. \(x=6\)

Zadanie nr 6 — maturalne.
Średnia arytmetyczna zestawu sześciu liczb \(2x, 4, 6, 8, 11, 13\) jest równa \(5\). Wynika stąd, że
A. \(x=-1\)
B. \(x=7\)
C. \(x=-6\)
D. \(x=6\)

Zadanie nr 7 — maturalne.
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
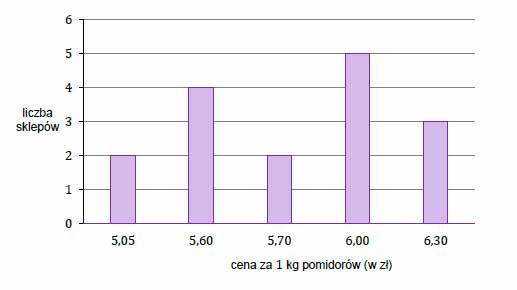
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
| 1. | Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa | |
| 2. | Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa |
A. 5,80 zł
B. 5,73 zł
C. 5,85 zł
D. 6 zł
E. 5,70 zł
Powiązane materiały
© medianauka.pl, 2011-08-13, A-1419
Data aktualizacji artykułu: 2023-07-24

 Średnia ważona
Średnia ważona Mediana
Mediana Dominanta
Dominanta Wariancja i odchylenie standardowe
Wariancja i odchylenie standardowe Pojęcia podstawowe statystyki
Pojęcia podstawowe statystyki