Nauka » Matematyka » Średnia arytmetyczna

Zadanie maturalne nr 24, matura 2015 (poziom podstawowy)

Treść zadania:

Średnia arytmetyczna zestawu danych: \(2, 4, 7, 8, 9\) jest taka sama jak średnia arytmetyczna zestawu danych: \(2, 4, 7, 8, 9, x\). Wynika stąd, że

A. \(x=0\)

B. \(x=3\)

C. \(x=5\)

D. \(x=6\)

Rozwiązanie zadania

Średnią arytmetyczną obliczamy ze wzoru:

\(\overline{x} = \frac{x_1+x_2+...+x_n}{n}\)

Ponieważ średnia arytmetyczna obu zestawów liczb (w pierwszym zestawie jest \(5\) liczb, w drugim liczb jest \(6\)) jest taka sama:

\(\frac{2+4+7+8+9}{5}=\frac{2+4+7+8+9+x}{6}\)

\(\frac{30}{5}=\frac{30+x}{6}/\cdot 30\)

\(6\cdot 30=5(30+x)/:5\)

\(36=30+x\)

\(x=6\)

Odpowiedź

Odpowiedź D

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

W zespole pracowników liczącym 30 osób 30% urodziło się w 1971 roku, 20% w 1980, 2 osoby w 1954 roku, 1 osoba w 1990, 3 osoby w 1972, 3 w 1973, 3 w 1975, 2 w 1979, 1 osoba w 1981. Jaka jest średnia wieku w zespole?

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Oblicz średnią arytmetyczną dziesięciu kolejnych liczb pierwszych.

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Średnia arytmetyczna sześciu liczb naturalnych \(31, 16, 25, 29, 27, x\) jest równa \(\frac{x}{2}\). Mediana tych liczb jest równa

A. 26

B. 27

C. 28

D. 29

Pokaż rozwiązanie zadania.

Zadanie nr 4 — maturalne.

W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.

tabela

Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Średnia arytmetyczna zestawu sześciu liczb \(2x, 4, 6, 8, 11, 13\) jest równa \(5\). Wynika stąd, że

A. \(x=-1\)

B. \(x=7\)

C. \(x=-6\)

D. \(x=6\)

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.

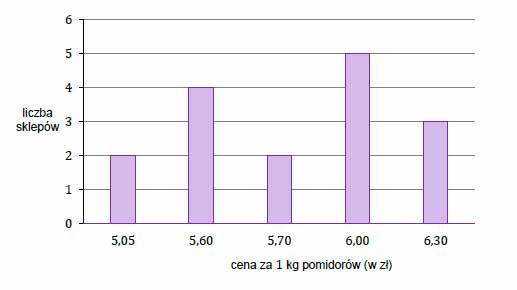
Zadanie 29, matura 2023, matematyka

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.

1.	Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa
2.	Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa

A. 5,80 zł

B. 5,73 zł

C. 5,85 zł

D. 6 zł

E. 5,70 zł

Pokaż rozwiązanie zadania.