Prawa Keplera

Zapamiętaj

Prawa Keplera:

Orbitą każdej planety jest elipsa, a Słońce leży w jednym z jej ognisk.
Promień wodzący planety zakreśla w równym czasie równe pola.
Kwadraty okresów obiegu planet są proporcjonalne do sześcianów ich średnich odległości od Słońca.

Wzory

\(\frac{T_{1}^{2}}{T_{2}^{2}}=\frac{r_{1}^{3}}{r_{2}^{3}}\)

Johannes Kepler na podstawie obserwacji przeprowadzonych przez Tycho Brache sformułował trzy prawa, które opisują ruch planet w naszym Układzie Słonecznym.

Pierwsze prawo Keplera

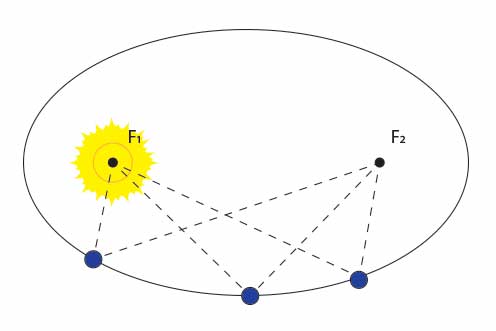
Pierwsze prawo Keplera opisuje kształt orbit planet.

Ruch wszystkich planet wokół Słońca odbywa się po orbitach eliptycznych, a Słońce znajduje się w jednym z ognisk elipsy.

Poniższy rysunek ilustruje 1 prawo Keplera.

Drugie prawo Keplera

Drugie prawo Keplera wynika z zasady zachowania momentu pędu.

Promień wodzący planety zakreśla równe pola w równych odstępach czasu

Poniższy rysunek ilustruje 2 prawo Keplera.

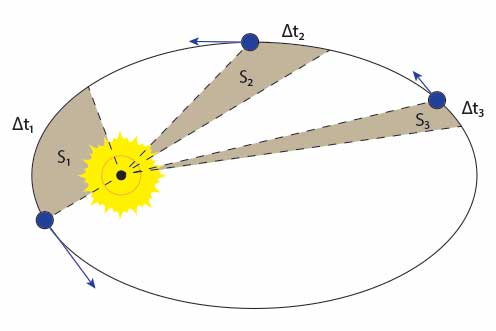
Prawo powyższe można zapisać za pomocą wzoru w następujący sposób:

Jeżeli \(\Delta t_1=\Delta t_2=\Delta t_3, to S_1=S_2=S_3\), gdzie \(\Delta t\) oznacza czas pomiaru, a S oznacza pole zakreślone przez planetę przez promień wodzący.

Trzecie prawo Keplera

Trzecie prawo Keplera podaje zależność między okresem obiegu planety wokół Słońca, a jej odległością od naszej gwiazdy.

Kwadraty okresów obiegu T planet są proporcjonalne do sześcianów ich średnich odległości r od Słońca.

\(\frac{T_{1}^{2}}{T_{2}^{2}}=\frac{r_{1}^{3}}{r_{2}^{3}}\)

Można także 3 prawo Keplera przedstawić w nieco inne formie, przekształcając powyższy wzór (mnożąc obie strony przez \(r_1^3\cdot T_2^2\).

Iloraz sześcianu średniej odległości r planety od Słońca i kwadratu okresu obiegu T jest wartością stałą.

\(\frac{r^{3}}{T^{2}}=C=const\)

Dla planet w Układzie Słonecznym wartość stałej \(C\), nazywanej heliocentryczną stałą grawitacji, wynosi:

\(C=\frac{G(M+m)}{4\pi^2}\approx \frac{GM}{4\pi^2}=3,36\cdot 10^{18} \ \frac{m^3}{s^3}\)

gdzie:

\(G\) - stała grawitacji,

\(M\) - masa Słońca,

\(m\) - masa planety.

Znając czasy obiegu planet wokół Słońca i ich średnie odległości od naszej gwiazdy, można wyznaczyć masę Słońca!

Zadanie

Oszacuj masę Słońca na podstawie danych dla Ziemi.

Rozwiązanie

Czas obiegu Ziemi wokół Słońca wynosi 1 rok, a odległość Ziemi od Słońca wynosi \(1\ AU\) (jednostka astronomiczna). Korzystając z III prawa Keplera mamy:

\(\frac{GM}{4\pi^2}=\frac{r^3}{T^2}/\cdot \frac{4\pi^2}{G}\)

\(M=\frac{4r^3\pi^2}{T^2G}\)

\(M=2\cdot 10^{30}kg\)

Ciekawostki

Prawa Keplera zostały sformułowane w 1609 roku w oparciu o dane empiryczne. Uzasadnienie tych praw wynika z powszechnego prawa ciążenia i podał je Isaac Newton w 1687 roku.

Pytania

Czy planety poruszają się po orbicie ze stałą szybkością?

Nie. Wynika to wprost z drugiego prawa Keplera. Najwolniej planeta porusza się w punkcie najdalej odległym od Słońca, najszybciej w punkcie najbliższym Słońcu.