Równanie fali

Będziemy rozpatrywać falę harmoniczną płaską, czyli taką, w której cząstki ośrodka wykonują drgania harmoniczne, a powierzchnie falowe są równoległe.

Jeżeli kierunek fali będzie zgodny z kierunkiem osi \(x\), a wychylenie cząsteczek ośrodka zgodne z osią y układu odniesienia, to:

\(y=Acos(\omega t+\phi )\)

gdzie:

\(y\) - wychylenie cząsteczek ośrodka materialnego,
\(A\) - amplituda,
\(t\) - czas,
\(\omega\) - częstość kołowa,
\(\phi\) - faza drgań.

Można tak dobrać układ odniesienia, aby faza \(\phi\) w chwili \(t=0\) była równa zeru (mamy więc \(y=Acos(\omega \cdot 0+0)=Acos 0\)).

Jeżeli v oznacza prędkość rozchodzenia się fali, to po czasie \(t=\frac{x}{v}\) punkt o współrzędnej \(x\) będzie miał taką samą fazę, tzn. \(y=Acos(\omega \cdot \frac{x}{v}+\phi)\) i wychylenia \(y\) drgającego punktu będą równe.

Mamy więc \(Acos0=Acos(\omega \cdot \frac{x}{v}+\phi )\), czyli

\(\omega \cdot \frac{x}{v}+\phi=0\)

\(\phi =-\omega \frac{x}{v}\)

Wielkość \(\frac{\omega}{v}\) to tak zwana liczba falowa.

Zatem otrzymujemy równanie harmoniczne fali płaskiej:

\(y=Acos(\omega t-kx)\)

lub z uwagi na parzystość funkcji cosinus:

\(y=Acos(kx-\omega t)\)

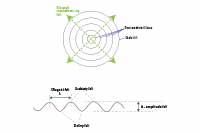
Długość fali to odległość między kolejnymi drgającymi punktami znajdujących się w tej samej fazie, czyli różniących się o kąt pełny \(2\pi \).

Zatem \(2\pi =k\lambda ;\), czyli \(\lambda =\frac{w\pi}{k}\).

Inne przydatne zależności to \(\lambda =\frac{2\pi v}{\omega}=vT\) i \(\lambda=\frac{v}{f}\).

Korzystając z tych zależności otrzymujemy inną postać równania fali harmonicznej:

\(y=Acos 2\pi (\frac{x}{\lambda}-\frac{t}{T})\)

Jeżeli chcemy analizować ruch fali w dowolnym kierunku, na przykład w kierunku wektora \(\vec{k}\), a położenie punktu w układzie współrzędnych opiszemy za pomocą wektora wodzącego \(\vec{r}\), to równanie falowe przyjmuje postać:

\(y=Acos (\vec{k}\cdot \vec{r} - \omega t)\)

Poziom zaawansowany

Funkcja falowa

Opiszemy przypadek rozchodzenia się fali w jednym kierunku.

Jeżeli przez \(\Psi\) oznaczymy zaburzenie ośrodka (na przykład wychylenie z położenia równowagi) , to ogólne równanie fali w chwili \(t=0\) opisze nam pena funkcja \(f(x)\), czyli \(\Psi =f(x)\). Po czasie \(t\) fala funkcja ta przyjmuje postać \(\Psi =f(x-vt)\).

Obliczymy różniczkę podwójną po czasie powyższej funkcji:

\(\frac{\partial^2\Psi}{\partial t^2}=v^2f''(x-vt)\)

\(\frac{1}{v^2}\frac{\partial^2\Psi}{\partial t^2}=f''(x-vt)\)

Obliczymy teraz różniczkę drugiego rzędu funkcji falowej po współrzędnej \(x\):

\(\frac{\partial^2\Psi}{\partial x^2}=f''(x-vt)\).

Mamy więc prawdziwą równość:

\(\frac{\partial^2\Psi}{\partial x^2}-\frac{1}{v^2}\frac{\partial^2\Psi}{\partial t^2}=0\)

To różniczkowe równanie ruchu falowego prawdziwe dla każdego rodzaju fali.

Można to równanie uogólnić na współrzędne przestrzenne:

\(\frac{\partial^2\Psi}{\partial x^2}+\frac{\partial^2\Psi}{\partial y^2}+\frac{\partial^2\Psi}{\partial z^2}-\frac{1}{v^2}\frac{\partial^2\Psi}{\partial t^2}=0\)

Używając operatora Laplace'a (laplasjan) równanie różniczkowe ruchu falowego w przestrzeni przyjmuje postać:

\(\nabla^2\Psi-\frac{1}{v^2}\frac{\partial^2\Psi}{\partial t^2}=0\)

Funkcja \(\Psi\) to tak zwana funkcja falowa.

Fala mechaniczna