II prawo Kirchhoffa

Drugie prawo Kirchhoffa brzmi następująco:

Suma algebraiczna zmian potencjałów w obwodzie zamkniętym jest równa zeru.

Powyższe prawo można zapisać za pomocą następującego wzoru:

\(\Sigma \varepsilon_i+\Sigma I_i R_i=0\)

Powyższy wzór możemy także przeczytać tak:

Suma wszystkich sił elektromotorycznych i spadków potencjału na oporach w oczku sieci jest równa zeru.

Często prawo to formułuje się także tak:

W obwodzie zamkniętym suma spadków napięć na wszystkich odbiornikach prądu musi być równa sumie napięć na źródłach napięcia.

\(\Sigma \varepsilon_i=\Sigma I_i R_i\)

Uwaga! Siły elektromotoryczne i spadki napięć na odbiornikach mogą mieć różne znaki, które należy uwzględnić w rozwiązywaniu obwodów zgodnie z przyjętą konwencją .

Prawa Kirchhoffa wykorzystuje się do obliczania napięć i natężeń prądu w rozgałęzionych obwodach elektrycznych. To tak zwane "rozwiązywanie obwodów". Przy ich stosowaniu należy pamiętać o następujących zasadach:

Warto zaznaczyć zwroty sił elektromotorycznych (od plusa do minusa) i spadki napięć na oporach.
Zaznaczamy strzałką kierunek przepływu prądu w oczku. Jeśli się okaże po rozwiązaniu równań, że natężenie jest ujemne, to oznacza, że zaznaczono błędnie kierunek przepływu prądu.
Przy zapisywaniu spadków potencjału obieramy zawsze ten kierunek obchodzenia danego oczka sieci, najlepiej przepływu prądu.
Zapisujemy tyle równań, ile jest różnych natężeń prądu w sieci. Niektóre równanie mogą się okazać zależne.

Przykład

Dany jest obwód przedstawiony na rysunku.

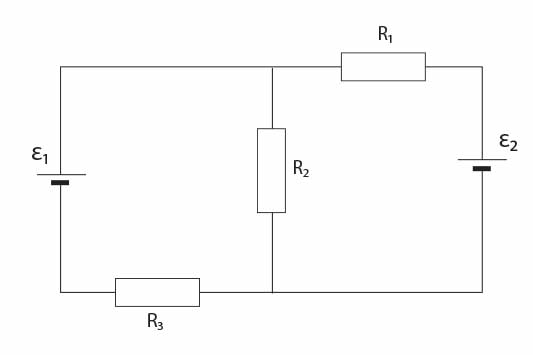
II prawo Kirchhoffa - przykład

Dane są także: \(\varepsilon_1,\ \varepsilon_2,\ R_1,\ R_2,\ R_3\), a opory wewnętrzne ogniw są pomijalne.

Prawa Kirchhoffa umożliwiają obliczenie natężeń prądów, jakie płyną w oczkach tego obwodu.

Wprowadźmy odpowiednie oznaczenia.

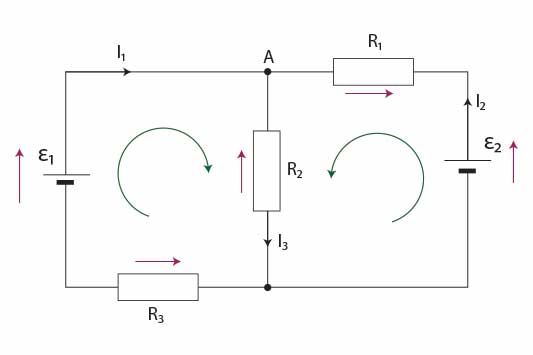
II prawo Kirchhoffa

Fioletowymi strzałkami zaznaczono kierunki spadków potencjałów na ogniwie i oporach. Zieloną strzałką zaznaczono kierunki przepływu prądów.

Dla węzła A możemy zapisać I prawo Kirchhoffa:

\(I_1+I_2=I_3\)

Zapiszemy teraz II prawo Kirchhoffa dla pierwszego z lewej oczka, zaczynając od ogniwa, idąc w kierunku wskazówek zegara. Jeżeli spadek potencjału jest przeciwny, składnik algebraicznej sumy zapisujemy wówczas ze znakiem minus. Mamy więc:

\(\varepsilon_1-I_3R_2-I_1R_3=0\)

W oczku z prawej zaczniemy również od ogniwa i pójdziemy w kierunku przepływu prądu.

\(\varepsilon_2-I_2R_1-I_3R_2=0\)

Otrzymaliśmy układ trzech równań, których rozwiązanie (bardzo żmudne) da nam w wyniku wartości natężeń prądów \(I_1, I_2, I_3\).

Siła elektromotoryczna

I prawo Kirchhoffa