Pole skalarne
Pole skalarne lub funkcja skalarna jest to funkcja, która każdemu punktowi \(P\) pewnego obszaru przyporządkowuje wartość liczbową \(U\), czyli skalar.
Pole skalarne \(U=U(P)\) można także opisywać za pomocą wektora wodzącego
\(\vec{r}=[x,y,z]\)
punktu \(P\) w danej przestrzeni (z ustalonym punktem odniesienia) jako:
\(U=U(\vec{r})\).
Jeżeli zaś pole skalarne zmienia się w czasie \(t\), możemy je opisać poprzez funkcję:
\(U=U(\vec{r},t)\).
Przykłady pól skalarnych
Przykładem pola skalarnego jest:
- pole temperatury, w którym każdemu punktowi rozpatrywanej przestrzeni przyporządkowujemy panującą tam temperaturę;
- pole potencjału;
- pole natężenia światła;
Pole centralne
Centralne pole skalarne jest szczególnym przypadkiem pola skalarnego, często spotykanym w fizyce. Mamy z nim do czynienia wówczas, jeżeli wszystkie punkty równoodległe od pewnego ustalonego punktu mają przypisaną tę samą liczbę.
Opisujemy je za pomocą funkcji: \(U=\Phi (x,y,z)\).
We współrzędnych kartezjańskich mamy:
\(U=U(\sqrt{x^2+y^2+z^2})\)
a we współrzędnych sferycznych:
\(U=U(r)\).
Izopowierzchnia
Izopowierzchnia jest to zbiór punktów pola skalarnego o takiej samej wartości liczbowej \(U=const\).
W przypadku dwóch wymiarów są to linie poziomicowe (np. na mapach wysokości lub temperatury), a w trzech wymiarach – powierzchnie.
Taka interpretacja pozwala łatwo zobaczyć, jak pole zmienia się w przestrzeni oraz gdzie przyjmuje wartości większe lub mniejsze.
Jak interpretować powyższy wykres?
Każda linia to linia poziomicowa (ta sama wartość pola). Środek (0,0) ma najmniejszą wartość. Im dalej od środka, tym większa wartość pola. Podobnie na mapach zaznacza się liniami daną wysokość (kontury gór).
Jak interpretować powyższy wykres?
Kolory oznaczają wartość pola. Skala po prawej pokazuje, jaka wartość odpowiada danemu kolorowi. Środek (ciemny) reprezentuje obszary o najmniejszej wartości.
Pole skalarne a pole wektorowe
Innym rodzajem pola jest pole wektorowe, o którym będzie mowa w odrębnym artykule.
Pole skalarne przypisuje każdemu punktowi przestrzeni jedynie wartość liczbową, natomiast pole wektorowe przypisuje wektor, czyli wielkość mającą zarówno wartość, jak i kierunek oraz zwrot.
Przykładowo: temperatura w pomieszczeniu jest polem skalarnym (ma tylko wartość),
pole grawitacyjne lub pole elektryczne są polami wektorowymi (mają wartość i kierunek działania).
Istnieje ścisły związek między tymi polami: z pola skalarnego można wyznaczyć pole wektorowe za pomocą operatora matematycznego zwanego gradientem.
Poniższa ilustracja porównuje (w uproszczony sposób i schematycznie) oba rodzaje pól.
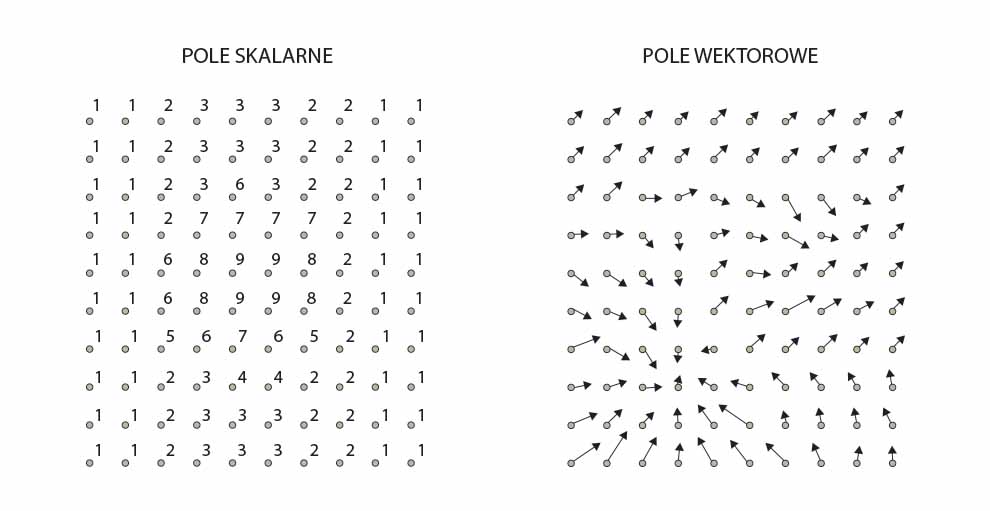
© medianauka.pl
Sens fizyczny pola skalarnego
W fizyce pojęcie pola wprowadza się, aby opisać oddziaływania w przestrzeni bez konieczności bezpośredniego kontaktu między ciałami. Zamiast mówić, że jedno ciało „działa na odległość” na inne, przyjmuje się, że w przestrzeni istnieje pole, które przekazuje to oddziaływanie.
Pole skalarne przypisuje każdemu punktowi przestrzeni pewną wielkość fizyczną (np. temperaturę lub potencjał), która opisuje stan tego pola w danym miejscu.
Dzięki temu fizyka może opisywać zjawiska w sposób lokalny – poprzez wartości pola w każdym punkcie przestrzeni, a nie przez bezpośrednie oddziaływania między obiektami.
Ciągłość i różniczkowalność pola
W fizyce zakłada się zazwyczaj, że pole skalarne jest ciągłe, co oznacza, że jego wartość zmienia się płynnie w przestrzeni (bez nagłych skoków).
Pole jest różniczkowalne, jeśli w każdym punkcie istnieje jego liniowe przybliżenie w otoczeniu tego punktu, opisujące lokalne zmiany pola.
Pozwala to na stosowanie narzędzi matematycznych, takich jak pochodne czy gradient.
Dzięki tym własnościom możliwe jest dokładne opisywanie zmian pola w przestrzeni oraz analizowanie zjawisk fizycznych w sposób ciągły i precyzyjny.
© medianauka.pl, 2021-08-23, A-4150/2354
Data aktualizacji artykułu: 2025-04-26
