Skrócenie Lorentza

Skrócenie Lorentza albo inaczej kontrakcja długości jest to w mechanice relatywistycznej zjawisko skracania odległości mierzonej w różnych układach odniesienia, będących względem siebie w ruchu.

W mechanice klasycznej mierzenie długości jest jednoznaczne w każdym układzie odniesienia. Mówimy, że odległość ma charakter absolutny.

W mechanice relatywistycznej odległość nie jest wielkością absolutną, zależy od układu odniesienia, w którym wykonujemy pomiar. Z im większa prędkością poruszają się względem siebie układy odniesienia, tym większe różnice powstaną w pomiarze odległości między dwoma punktami.

Skrócenie Lorentza wynosi:

\(\Delta x=\Delta x'\sqrt{1-\frac{u^2}{c^2}}\)

Zauważmy, że jeżeli tylko prędkość poruszania się jednego układu względem drugiego nie jest zerowa (\(u\gt 0\), to zawsze mamy do czynienia ze skróceniem odległości między dwoma punktami w układzie obserwatora, względem którego poruszają się te dwa punkty, a między którymi mierzymy tę odległość. To jest właśnie skrócenie Lorentza, wynikające wprost z transformacji Lorentza.

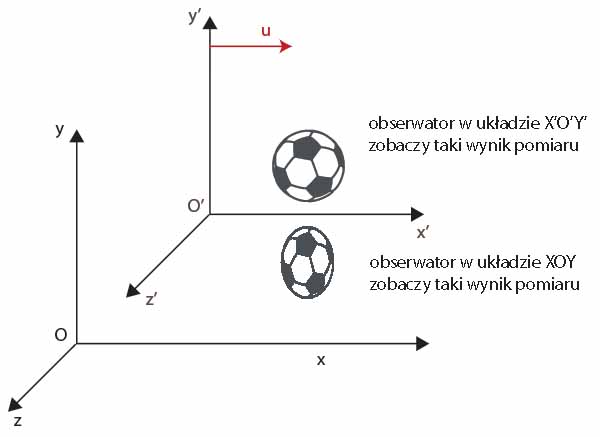
Zjawisko to ilustruje poniższy rysunek. Obserwator w układzie \(U'\) zobaczy kulistą piłkę. Inny obserwator, znajdujący się w układzie \(U\) będzie tę samą piłkę postrzegał jako jajowaty twór. Ten sam obiekt - dwie różne obserwacje.

Ciekawostki

Jeżeli układ odniesienia z dwoma punktami porusza się wzdłuż naszego układu odniesienia wzdłuż osi \(OX\), to skracają się jedynie wymiary wzdłuż tej osi. Jeżeli więc w tym przypadku skraca się długość, to wysokość i szerokość pozostają bez zmian!

Przykład

Pan Jan zmierzył stojąc na ulicy długość parasola (poziomo) i otrzymał wynik 70 cm. O ile zmieni się wynik, gdy pan Jan spróbuje zmierzyć go, gdy jego parasol odjedzie taksówką z prędkością 60 km/h, leżąc poziomo na tylnym siedzeniu? Jaki wynik uzyska siedząc w tej taksówce? Z jaką prędkością musiałby się poruszać samochód, aby długość parasola wynosiła 69 cm?

Rozwiązanie

Wykonując pomiar na ulicy i w taksówce Pan Jan otrzyma ten sam wynik, gdyż w obu przypadkach parasol nie porusza się względem niego. W przypadku, gdy parasol odjeżdża w samochodzie mamy do czynienia ze skróceniem Lorentza. Podstawmy dane:

\(\Delta x'=70\ cm\)

\(u=60 \frac{km}{h} \approx 16,67 \frac{m}{s}\)

\(u^2 \approx 277,78 \frac{m^2}{s^2}\)

\(c^2 \approx 8,988 \cdot 10^{16} \frac{m^2}{s^2}\)

\(\frac{u^2}{c^2} \approx 3,09 \cdot 10^{-15}\)

Zatem

\(1-\frac{u^2}{c^2} \approx 0,999 999 999 999 997\)

Pierwiastek z tej wielkości jest jeszcze mniejszą liczbą, zatem pan Jan nie zauważy w ogóle zmniejszenia długości parasola przy tak małej prędkości taksówki. Nie zdoła tego nawet zmierzyć.

To z jaką prędkością musiałby się poruszać nasz samochód, aby zauważyć centymetrowe skrócenie długości?

Przekształćmy nasz wzór:

\(\Delta x=\Delta x'\sqrt{1-\frac{u^2}{c^2}}/:\Delta x'\)

\(\frac{\Delta x}{\Delta x'}=\sqrt{1-\frac{u^2}{c^2}}/^2\)

\((\frac{\Delta x}{\Delta x'})^2=1-\frac{u^2}{c^2}\)

\(\frac{u^2}{c^2}=1-(\frac{\Delta x}{\Delta x'})^2 / \cdot c^2\)

\(u^2=c^2[1-(\frac{\Delta x}{\Delta x'})^2]\)

\( u=c\sqrt{1-(\frac{\Delta x}{\Delta x'})^2}\)

Podstawiając dane:

\(\frac{\Delta x}{\Delta x'}=0,9857\),

\(c \approx 300 000 km/s\),

otrzymamy:

\(v \approx 0,1685 c \approx 50 553 km/s\).

To sporo jak na samochód.

Jednak w świecie cząstek elementarnych jak i w kosmosie prędkości relatywistyczne nie należą do rzadkości.

Pytania

Ile wynosi skrócenie Lorentza dla prędkości światła?

Wprost ze wzoru wynika, że \(\Delta x=0\)!

Dylatacja czasu

Transformacja Lorentza