Dlaczego często kroimy kiełbasę pod kątem?

Krojenie plasterków kiełbasy, salami lub innej wędliny jest dość częstą praktyką. Ma ona na celu ukrojenie zwyczajnie większych plastrów. Jak to możliwe i jak wielkie mogą być plastry? Z pomocą przychodzi twierdzenie Pitagorasa.

To jedno z kuchennych zastosowań matematyki.

Poniższy rysunek przedstawia model kiełbasy, krojonej pod kątem. Jeżeli kiełbasa może być uznana jako walec o średnicy podstawy d, to jeżeli będziemy naszą kiełbasę kroić pod kątem prostym, plasterki będą kołami o średnicy d.

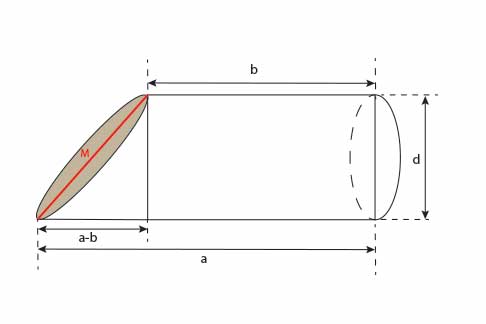
Kiełbasa

Jeśli zaś kroić kiełbasę pod pewnym kątem, plasterki zaczną przypominać elipsę. Oś wielką oznaczmy przez M. Korzystając z twierdzenia Pitagorasa otrzymamy:

$M=\sqrt{(a-b)^2+d^2}$

Średnica kiełbasy jest stała. Z powyższego wzoru widać, że gdy b zdąża do zera, oś elipsy zbliża się coraz bardziej do wartości a. Zatem plastry kiełbasy mogą mieć maksymalnie długość zbliżoną do

$M=\sqrt{a^2+d^2}$ .

Długość plastra jest zatem ograniczona wyłącznie długością kiełbasy.

Plastry mają podczas krojenia pod kątem większą powierzchnię - stają się bardziej pożywne, a kształt plastra zamiast koła przybiera postać elipsy, co może mieć także znaczenie estetyczne.

Ciekawostki

Kakaowiec i pokarm bogów

Ciekawostki

Dlaczego gwiazdy zataczają okręgi wokół Gwiazdy Polarnej?

Ciekawostki

Czy można spowolnić fotony?

Ciekawostki

Zobacz więcej

Zobacz też

Twierdzenie Pitagorasa