Ruch jednostajnie przyspieszony

Ruch jednostajnie przyspieszony prostoliniowy jest to ruch ze stałym przyspieszeniem po linii prostej, a prędkość i przyspieszenie mają ten sam zwrot (a=constans).

Ruch ten jest szczególnym przypadkiem ruchu jednostajnie zmiennego, w którym wektor przyspieszenia ma ten sam zwrot co wektor prędkości, a to oznacza, że w kolejnych, równych odcinkach czasu następuje taki sam przyrost prędkości (wartości prędkości, prędkość stale wzrasta).

Zapamiętaj

Ruch jednostajnie przyspieszony prostoliniowy - to ruch ze stałym przyspieszeniem po linii prostej, a prędkość i przyspieszenie mają ten sam zwrot.

$x=x_0+v_0t+\frac{1}{2}at^2$

Poniżej wykres zależności a(t) w ruchu jednostajnie przyspieszonym prostoliniowym.

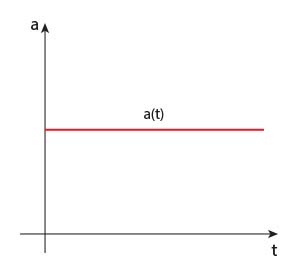
Zależność przyspieszenia od czasu w ruchu jednostajnie przyspieszonym

W artykule Równanie ruchu zostały wyprowadzone wzory dla ruchu jednostajnie przyspieszonego.

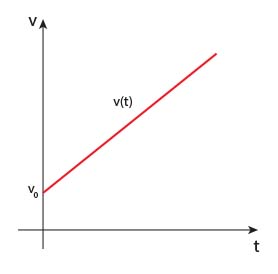
Równanie zależności v(t) w ruchu jednostajnie przyspieszonym prostoliniowym jest następujące:

Poniżej została zilustrowana na wykresie zależność v(t) w ruchu jednostajnie przyspieszonym prostoliniowym.

Zależność v(t) w ruchu jednostajnie przyspieszonym prostoliniowym

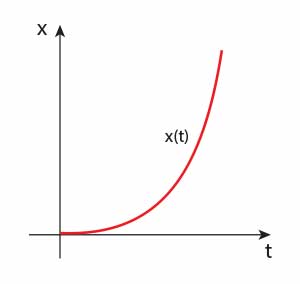
Równanie zależności x(t) w ruchu jednostajnie przyspieszonym prostoliniowym jest następujące:

$x=x_0+v_0t+\frac{1}{2}at^2$

Poniżej została zilustrowana na wykresie zależność x(t) w ruchu jednostajnie przyspieszonym prostoliniowym (wykresem tej zależności jest parabola - jedna gałąź).

zależność x(t) w ruchu jednostajnie przyspieszonym prostoliniowym

Drogi przebyte w ruchu jednostajnie przyspieszonym w kolejnych, takich samych odcinkach czasu mają się do siebie jak kolejne liczby nieparzyste: s₁:s₂:s₃:...=1:3:5:...

Uwaga! Nie możemy powiedzieć, że w ruchu przyspieszonym przyspieszenie jest dodatnie lub, że wartość przyspieszenia jest dodatnia. Znak przy wartości przyspieszenia informuje nas tylko o zgodności zwrotu wektora przyspieszenia ze zwrotem wektora prędkości.

Inne zagadnienia z tej lekcji

Równanie ruchu

Ruch jednostajny prostoliniowy

Ruch jednostajnie opóźniony prostoliniowy