Rzut ukośny

Rzut ukośny jest to ruch ciała w polu grawitacyjnym, któremu nadano prędkość początkową pod pewnym kątem do poziomu.

Podobnie jak w przypadku rzutu poziomego, jest to przykład ruchu w dwóch wymiarach. W takim przypadku ruch ciała musimy rozłożyć na dwa niezależne ruchy, które odbywają się w kierunkach wyznaczonych przez układ odniesienia. Spójrz na rysunek.

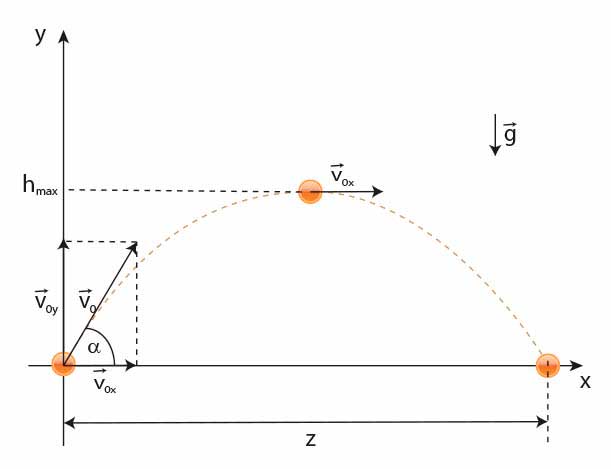
rzut ukośny

Zapamiętaj

Maksymalna wysokość w rzucie ukośnym:

$h_{max}=\frac{v_0^2}{2g}\sin^2\alpha$

Czas ruchu w rzucie ukośnym:

Zasięg rzutu ukośnego:

$z=\frac{v_0^2}{g} sin2\alpha$

Maksymalny zasięg rzutu uzyskuje się dla kąta 45°.

Korzystając z funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym możemy zapisać następujące relacje między składowymi prędkości początkowej a prędkością początkową:

$v_{0y}=v_0sin\alpha\\ v_{0x}=v_0cos\alpha$

W naszych rozważaniach pomijamy opory powietrza. Składowa pozioma prędkości jest stała, gdyż w kierunku osi Ox nie występuje żadne przyspieszenie, natomiast składowa pionowa prędkości zmienia się: najpierw maleje do osiągnięcia maksymalnej wysokości, po czym zaczyna rosnąć aż do osiągnięcia poziomu ziemi, z którą jest związany nasz układ odniesienia. Wektor przyspieszenia jest zwrócony przeciwnie do osi Oy, zatem składową pionową przyspieszenia będziemy zapisywać ze znakiem minus. Wektor składowej pionowej prędkości jest zgodny ze zwrotem osi Oy, zatem składową tą zapisujemy w równaniach ruchu ze znakiem plus.

W dowolnej chwili ruchu wartość prędkości, czyli szybkość obliczymy ze wzoru:

$v=\sqrt{v_x^2+v_y^2}$

gdzie zgodnie z równaniami ruchu:

$v_x=v_{0x}\\v_y=y_{0y}-gt$

Jeżeli zechcemy obliczyć maksymalną wysokość, na jaką wzniesie się ciało, to wiemy, że położenie początkowe w układzie odniesienia jest równe zeru, końcowe h_max, a składowa pionowa przyspieszenia będzie zapisana ze znakiem minus z uwagi na przeciwny zwrot tego wektora do zwrotu osi układu odniesienia. Czas wznoszenia oznaczymy przez t_w:

$h_{max}=v_{0y}t_w-\frac{1}{2}gt_w^2$

Czas wznoszenia wynosi:

$t_w=\frac{v_0}{g}$

(Wyprowadzenie powyższego wzoru tutaj). Podstawiając czas wznoszenia do wzoru na maksymalną wysokość oraz wzór na składową pionową wektora prędkości otrzymamy:

$h_{max}=v_{0y}t_w-\frac{1}{2}gt_w^2\\ h_{max}=v_{0y}\cdot (\frac{v_{0y}}{g})-\frac{1}{2}g\cdot \frac{v_{0y}^2}{g^2}\\h_{max}=\frac{v_{0y}^2}{2g}\\h_{max}=\frac{v_0^2}{2g}\sin^2\alpha$

Zatem maksymalna wysokość na jaką się wzniesie ciało w rzucie ukośnym wynosi:

$h_{max}=\frac{v_0^2}{2g}\sin^2\alpha$

Aby obliczyć czas ruchu (spadania) t_s w rzucie ukośnym stosujemy równanie ruchu zależności położenia od czasu. Położenie początkowe wynosi 0, końcowe również 0, gdyż ciało spada podczas tego ruchu w efekcie na ziemię. Mamy więc:

wzór

Przypadek t_s=0 nas nie interesuje, bo w tej chwili ciało zaczyna swój ruch.

Zatem czas ruchu ciała w rzucie ukośnym wynosi:

W kierunku osi Ox ciało porusza się ruchem jednostajnym. Ruch trwa dokładnie t_s. W prosty sposób można więc wyznaczyć zasięg ruchu:

wzór

Zasięg ruchu w rzucie ukośnym dany jest wzorem:

$z=\frac{v_0^2}{g} sin2\alpha$

Z powyższego wzoru wynika, że maksymalny zasięg rzutu można uzyskać dla wartości sin2α=1, czyli dla α=45°.

Jeżeli wziąć pod uwagę opór powietrza, to ciało porusza się nie po paraboli, a po krzywej, która nosi nazwę krzywej balistycznej. W takim przypadku zasięg rzutu jest nieco mniejszy od wyżej wyznaczonego.

Inne zagadnienia z tej lekcji

Spadek swobodny

Spadek swobodny jest to ruch ciała w polu grawitacyjnym upuszczonego z pewnej wysokości na ziemię. Spadek swobodny jest przykładem ruchu jednostajnie przyspieszonego prostoliniowego z przyspieszeniem a=g=const.

Rzut pionowy

Rzut pionowy jest to ruch ciała w polu grawitacyjnym pionowo do góry lub pionowo w dół z pewnej wysokości na ziemię. Rzut pionowy jest przykładem ruchu jednostajnie przyspieszonego prostoliniowego z przyspieszeniem g=const.

Rzut poziomy

Rzut poziomy jest to ruch ciała w polu grawitacyjnym, wyrzuconego poziomo z pewną prędkością początkową z danej wysokości. Jest to doskonały przykład ruchu w dwóch wymiarach. Wyprowadzenie wzoru na wzór na zasięg rzutu poziomego.

Czy baletnica zawisa w powietrzu podczas tańca?

Gdy obserwuje się baletnicę podczas tańca, to wydaje się, że podczas skoku zdaje się ona zawisać na chwilę w powietrzu lub przebywać w podskoku nienaturalnie długo? Jak to się dzieje?