Spadek swobodny

Spadek swobodny albo spadanie swobodne jest to ruch ciała w polu grawitacyjnym upuszczonego z pewnej wysokości na ziemię. Spadek swobodny jest przykładem ruchu jednostajnie przyspieszonego prostoliniowego z przyspieszeniem a=g=const. Przyspieszenie to nazywamy przyspieszeniem ziemskim i oznaczamy je literą g.

spadek swobodny Wszystkie ciała w polu grawitacyjnym Ziemi spadają z takim samym przyspieszeniem. Dziwne? Przecież cegła spada inaczej niż piórko! Otóż wszystkiemu winny jest opór powietrza, a więc działanie pewnych sił, o których nic jeszcze nie mówiliśmy. Jednak gdyby wypompować powietrze z otoczenia albo wykonać doświadczenie na Księżycu, cegła i piórko spadałoby tak samo.

W spadku swobodnym czas spadania t_s ciała upuszczonego z wysokości h możemy obliczyć ze wzoru:

$t_s=\sqrt{\frac{2h}{g}}$

Z kolei szybkość ciała w chwili zderzenia z podłożem v_k ciała upuszczonego z wysokości h możemy obliczyć ze wzoru:

$v_k=\sqrt{2hg}$

Wyprowadzenie wzorów

Wyprowadzimy powyższe zależności. Wyprowadzenie to będzie świetnym przykładem zastosowania równania ruchu jednostajnie przyspieszonego. Wprowadzimy układ odniesienia związany z podłożem i zrobimy szkic z oznaczeniami.

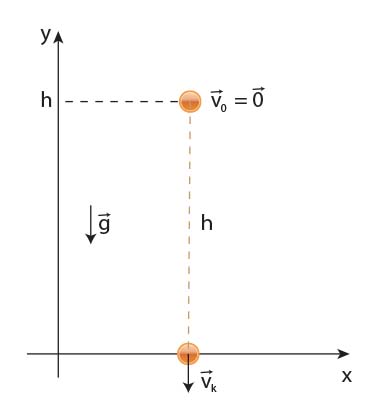
układ odniesienia - spadek swobodny

Korzystamy z równania ruchu:

$\vec{r}=\vec{r_0}+\vec{v_0}t+\frac{1}{2}\vec{g}t^2$

Uwaga! Prędkość początkowa jest równa zeru (puszczamy swobodnie ciało, nie nadajemy mu żadnej prędkości). Położenie początkowe jest równe h, a końcowe 0. Przyspieszenie skierowane jest przeciwnie do osi układu odniesienia, zapisujemy je więc ze znakiem minus. Ruch odbywa się tylko wzdłuż jednej osi układu odniesienia, możemy więc posługiwać sie skalarami (jedną współrzędna wektorów). Nasze równanie ruchu y(t) przyjmuje postać:

$0=h+0\cdot t-\frac{1}{2}gt^2\\h=\frac{1}{2}gt^2/\cdot \frac{2}{g}\\ \frac{2h}{g}=t^2\\t=\sqrt{\frac{2h}{g}}$

Korzystamy z równania ruchu:

$\vec{v}=\vec{v_0}+\vec{g}t$

Uwaga! W naszym przypadku końcowa prędkość jest oznaczona jako v_k i jest skierowane przeciwnie do osi układu odniesienia, zapisujemy je więc ze znakiem minus. Prędkość początkowa jest równa zeru. Przyspieszenie skierowane jest przeciwnie do osi układu odniesienia, zapisujemy je więc ze znakiem minus. Ruch odbywa się tylko wzdłuż jednej osi układu odniesienia, możemy więc posługiwać sie skalarami (jedną współrzędna wektorów). Nasze równanie ruchu v(t) przyjmuje postać:

$-v_k=0-gt\\v_k=gt\\v_k=g\sqrt{\frac{2h}{g}}\\v_k=\sqrt{\frac{2hg^2}{g}}\\v_k=\sqrt{2hg}$

Inne zagadnienia z tej lekcji

Rzut pionowy

Rzut pionowy jest to ruch ciała w polu grawitacyjnym pionowo do góry lub pionowo w dół z pewnej wysokości na ziemię. Rzut pionowy jest przykładem ruchu jednostajnie przyspieszonego prostoliniowego z przyspieszeniem g=const.

Rzut poziomy

Rzut poziomy jest to ruch ciała w polu grawitacyjnym, wyrzuconego poziomo z pewną prędkością początkową z danej wysokości. Jest to doskonały przykład ruchu w dwóch wymiarach. Wyprowadzenie wzoru na wzór na zasięg rzutu poziomego.

Rzut ukośny

Rzut ukośny jest to ruch ciała w polu grawitacyjnym, któremu nadano prędkość początkową pod pewnym kątem do poziomu. Jest to przykład ruchu w dwóch wymiarach. W takim przypadku ruch ciała musimy rozłożyć na dwa niezależne ruchy, które odbywają się w kierunkach wyznaczonych przez układ odniesienia.

Czy w spadającej windzie wchodzimy w stan nieważkości?

Gdy winda zerwie się nagle i zacznie spadać razem z nami będziemy podczas spadania w stanie nieważkości? Czy aby zminimalizować obrażenia należy podskoczyć tuż przed uderzeniem o podłoże?

Dlaczego kanapka spada masłem w dół?

Czy to prawda, że kanapka zrzucona ze stołu spada zawsze masłem w dół? Jeżeli tak, to dlaczego? Czy ma tu zastosowanie prawo Mutphy'ego?

Czy baletnica zawisa w powietrzu podczas tańca?

Gdy obserwuje się baletnicę podczas tańca, to wydaje się, że podczas skoku zdaje się ona zawisać na chwilę w powietrzu lub przebywać w podskoku nienaturalnie długo? Jak to się dzieje?