Zadanie - równanie dwusiecznej kąta
Treść zadania:
Znaleźć równanie dwusiecznej kątów wyznaczonych przez proste o równaniach \(y=-\frac{3}{4}x+\frac{1}{2}\) i \(y=\frac{4}{3}x+\frac{5}{3}\).
Rozwiązanie zadania
Wszystkie punkty dwusiecznej kąta mają taką samą odległość od ramion kąta. Ponieważ ramiona kąta pokrywają się z równaniami danych prostych, problem sprowadza się do zastosowania wzoru na odległość punktu \(P=(x,y)\) od prostej \(Ax+By+C=0\), która wyrażona jest wzorem:
\(d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)Trzeba zmienić postaci równań prostych z równań kierunkowych na postać występującą w powyższym wzorze:
\(y=-\frac{3}{4}x+\frac{1}{2}/\cdot 4\)
\(4y=-3x+2\)
\(3x+4y-2=0\)
Dla drugiej prostej:
\(y=\frac{4}{3}x+\frac{5}{3}/\cdot 3\)
\(3y=4x+5\)
\(-4x+3y-5=0\)
Odległość dowolnego punktu \(P=(x,y)\) dwusiecznej kąta od prostej \(y=-\frac{3}{4}x+\frac{1}{2}\) będzie więc równa:
\(3x+4y-2=0\)
\(A=3, \ B=4,\ C=-2\)
\(P=(x,y)\)
\(d_1=\frac{|3x+4y-2|}{\sqrt{3^2+4^2}}=\frac{|3x+4y-2|}{\sqrt{25}}=\frac{|3x+4y-2|}{5}\)
Odległość dowolnego punktu \(P=(x,y)\) dwusiecznej kąta od prostej\(y=\frac{4}{3}x+\frac{5}{3}\) będzie więc równa:
\(-4x+3y-5=0\)
\(A=-4, \ B=3,\ C=-5\)
\(P=(x,y)\)
\(d_2=\frac{|-4x+3y-5|}{\sqrt{(-4)^2+3^2}}=\frac{|-4x+3y-5|}{\sqrt{25}}=\frac{|-4x+3y-5|}{5}\)
Jak wcześniej wspominano dla punktów dwusiecznej odległości te są równe, więc:
\(d_1=d_2\)
\(\frac{|3x+4y-2|}{5}=\frac{|-4x+3y-5|}{5}/\cdot 5\)
\(|3x+4y-2|=|-4x+3y-5|\)
Ponieważ mamy do czynienia z wartościami bezwzględnymi musimy rozpatrzyć kilka przypadków w zależności od wartości wyrażeń pod wartością bezwzględną.
1) Dla wartości wyrażeń pod wartością bezwzględną większych od zera lub równych zero możemy opuścić wartości bezwzględne (ponieważ mamy tutaj równanie z dwoma niewiadomymi warunek ten będzie spełniony dla wszystkich punktów jednego kąta z czterech wyznaczonego przez dwie proste):
\(3x+4y-2=-4x+3y-5\)
\(4y-3y=-4x-3x-5+2\)
\(y=-7x-3\)
2) Dla wartości wyrażeń pod wartością bezwzględną mniejszych od zera możemy opuścić wartości bezwzględne, jeżeli zmienimy znaki obu wyrażeń na przeciwne:
\(-(3x+4y-2)=-(-4x+3y-5)/\cdot(-1)\)
\(4y-3y=-4x-3x-5+2\)
\(y=-7x-3\)
Otrzymaliśmy to samo równanie.
3) i 4) Dla wartości wyrażeń pod wartością bezwzględną mniejszych od zera w jednym przypadku i większych lub równych zero w drugim przypadku (otrzymamy ten sam wynik) możemy opuścić wartości bezwzględne, jeżeli zmienimy znaki jednego z wyrażeń na przeciwny:
\(-(3x+4y-2)=-4x+3y-5\)
\(-4y-3y=3x-4x-5-2\)
\(-7y=-x-7/:(-7)\)
\(y=\frac{1}{7}x+1\)
Sprawdźmy nasze rozwiązanie, sporządzając szkic wykresu:
Odpowiedź
\(y=-7x-3, \ y=\frac{1}{7}x+1\)© medianauka.pl, 2011-02-19, ZAD-1174


Zadania podobne

Zadanie nr 1 — maturalne.
Dwusieczne czworokąta \(ABCD\) wpisanego w okrąg przecinają się w czterech różnych punktach: \(P, Q, R, S\) (zobacz rysunek).
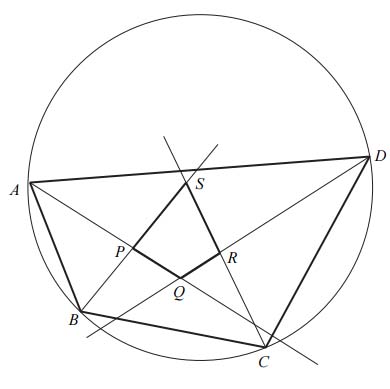
Wykaż, że na czworokącie \(PQRS\) można opisać okrąg.

