Zadanie maturalne nr 14, matura 2022 - poziom rozszerzony
Treść zadania:
Punkt \(A=(−3,2)\) jest wierzchołkiem trójkąta równoramiennego \(ABC\), w którym \(|AC|=|BC|\). Pole tego trójkąta jest równe 15. Bok \(BC\) zawarty jest w prostej o równaniu \(y=x-1\). Oblicz współrzędne wierzchołków \(B\) i \(C\) tego trójkąta.
Rozwiązanie zadania
Sporządzamy rysunek poglądowy:
Obliczmy wysokość trójkąta ABC jako odległość punktu A od danej prostej.
W tym celu przekształcamy nasze równanie prostej do postaci:
\(x-y-1=0\)
\(h=\frac{|-3-2-1|}{\sqrt{2}}=\frac{6}{\sqrt{2}}= \frac{6\sqrt{2}}{2}=3\sqrt{2}\)
Pole naszego trójkąta jest równe:
\(P=\frac{1}{2}|BC|\cdot h\)
\(15=\frac{1}{2}|BC|\cdot 3\sqrt{2}\)
\(|BC|\cdot 3\sqrt{2}=30/:3\sqrt{2}\)
\(|BC|=\frac{10}{\sqrt{2}}=5\sqrt{2}\)
Z warunków zadania wynika, że mamy do czynienia z trójkątem równoramiennym, więc:
\(|AC|=5\sqrt{2}\)
Niech punkt \(C\) ma współrzędne \(C=(x_C,y_C)\). Ponieważ punkt ten leży na prostej \(y=x-1\), to \(C=(x_C,x_C-1)\).
\(|AC|=\sqrt{(x_C-(-3))^2+(x_C-1-2)^2}=5\sqrt{2}\)
\(\sqrt{(x_C+3)^2+(x_C-3)^2}=5\sqrt{2}/^2\)
\(x_C^2+6x_C+9+x_C^2-6x_C+9=50\)
\(2x_C^2-32=0\)
\(x_C^2-16=0\)
\((x_C-4)(x_C+4)=0\)
\(x_C=4\) lub \(x_C=-4\)
\(C=(4,2)\) lub \(C=(-4,-5)\)
Poszukamy współrzędnych punktu \(B=(x_B,x_B-1)\).
Przypadek 1
Dla \(C=(4,3)\) mamy:
\(|BC|=\sqrt{(4-x_B)^2+(3-(x_B-1))^2}=5\sqrt{2}\)
\(\sqrt{(4-x_B)^2+(4-x_B)^2}=5\sqrt{2}/^2\)
\(2(4-x_B)^2=50\)
\((4-x_B)^2=25\)
\(4-x_B=5\) lub \(4-x_B=-5\)
\(-x_B=1\) lub \(-x_B=-9\)
\(x_B=-1\) lub \(x_B=9\)
\(B=(-1,-2)\) lub \(B=(9,8)\)
Przypadek 2
Dla \(C=(-4,-5)\) mamy:
\(|BC|=\sqrt{(-4-x_B)^2+(-5-(x_B-1))^2}=5\sqrt{2}\)
\(\sqrt{(-4-x_B)^2+(-4-x_B)^2}=5\sqrt{2}/^2\)
\(2(-4-x_B)^2=50\)
\((-4-x_B)^2=25\)
\(-4-x_B=5\) lub \(-4-x_B=-5\)
\(-x_B=9\) lub \(-x_B=-1\)
\(x_B=-9\) lub \(x_B=1\)
\(B=(1,0)\) lub \(B=(-9,-10)\)
Odpowiedź
Warunki zadania spełniają następujące pary punktów:
- \(C=(4,3), B=(-1,-2)\)
- \(C=(4,3), B=(9,8)\)
- \(C=(-4,-5), B=(1,0)\)
- \(C=(-4,-5), B=(-9,-10)\)
© medianauka.pl, 2023-04-29, ZAD-4892


Zadania podobne

Zadanie nr 1 — maturalne.
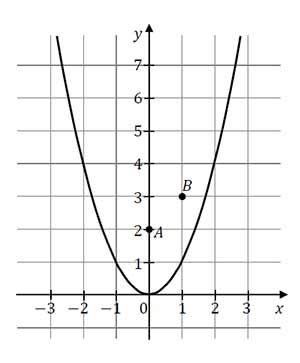
Dane są parabola o równaniu y = x2 oraz punkty A = (0, 2) i B = (1, 3) (zobacz rysunek). Rozpatrujemy wszystkie trójkąty ABC, których wierzchołek C leży na tej paraboli. Niech m oznacza pierwszą współrzędną punktu C.
a) Wyznacz pole P trójkąta ABC jako funkcję zmiennej m.
b) Wyznacz wszystkie wartości m, dla których trójkąt ABC jest ostrokątny.