Zadanie - obrót
Treść zadania:
Znaleźć obraz wykresu funkcji \(y=|x|\) w obrocie dookoła początku układu współrzędnych o kąt \(45°\).
 Rozwiązanie zadania
Rozwiązanie zadania
W obrocie dookoła punktu /(O/) (początek układu współrzędnych) o kąt skierowany \(\angle \vec{\alpha}\) obrazem pewnego punktu \(P=(x,y)\) jest punkt \(P'=(x',y')\). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
\(x=x'\cos{\alpha}+y'\sin{\alpha} \)
\(y=-x'\sin{\alpha}+y'\cos{\alpha}\)
oraz
\(x'=x\cos{\alpha}-y\sin{\alpha} \)
\(y'=x\sin{\alpha}+y\cos{\alpha}\)
Zatem zależność między współrzędnymi dowolnego punktu wykresu i jego obrazu jest następująca:
\(x=x'\cos{\alpha}+y'\sin{\alpha} =x'\cos{45^o}+y'\sin{45^o}=x'\cdot \frac{\sqrt{2}}{2}+y'\cdot \frac{\sqrt{2}}{2}\)
\(y=-x'\sin{\alpha}+y'\cos{\alpha}=-x'\sin{45^o}+y'\cos{45^o}=-x'\cdot \frac{\sqrt{2}}{2}+y'\cdot \frac{\sqrt{2}}{2}\)
Mamy tutaj do czynienia z wartością bezwzględną. Zgodnie z jej definicją mamy:
\(x=\begin{cases} x, \ dla \ x\geq 0 -x, \ dla \ x<0 \end{cases}\)
Rozpatrujemy więc dwa przypadki:
\(1) x\geq 0\)
\(\frac{\sqrt{2}}{2}x'+\frac{\sqrt{2}}{2}y'\geq 0/:\frac{\sqrt{2}}{2}\)
\(x'+y'\geq 0\)
\(y'\geq -x\)
Podstawiamy te zależności do naszego wzoru:
\(y=|x|=x\)
\(-x'\cdot \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}y'= \frac{\sqrt{2}}{2}x'+ \frac{\sqrt{2}}{2}y'/:\frac{\sqrt{2}}{2}\)
\(-x'+y'=x'+y'\)
\(-2x'=0/:(-2)\)
\(x'=0\)
Aby lepiej zrozumieć powyższy warunek i rachunki warto sporządzić szkic rysunku.
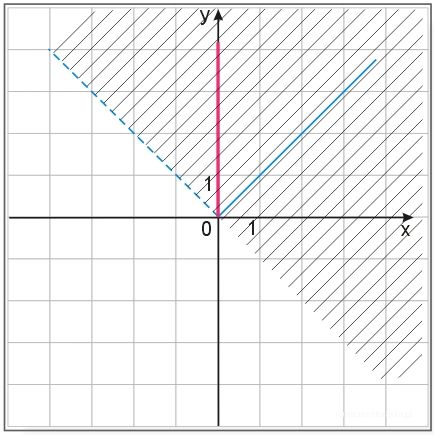
Kolorem niebieskim zaznaczono fragment wykresu funkcji \(y=|x|\) dla x większych lub równych zero. Obrazu prostej szukamy tylko w dla \(y'\geq -x'\) (obszar zakreskowany), a więc jest to prosta \(x=0\) tylko w zakreskowanym obszarze
Rozpatrujemy drugi przypadek:
\(2) x<0\)
\(\frac{\sqrt{2}}{2}x'+\frac{\sqrt{2}}{2}y'< 0/:\frac{\sqrt{2}}{2}\)
\(x'+y'<0\)
\(y'<-x'\)
Podstawiamy te zależności do naszego wzoru:
\(y=|x|=-x\)
\(-x'\cdot \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}y'=-\frac{\sqrt{2}}{2}x'-\frac{\sqrt{2}}{2}y'/:\frac{\sqrt{2}}{2}\)
\(-x'+y'=-x'-y'\)
\(-2y'=0/:(-2)\)
\(y'=0\)
Aby lepiej zrozumieć powyższy warunek i rachunki warto sporządzić drugi szkic rysunku.
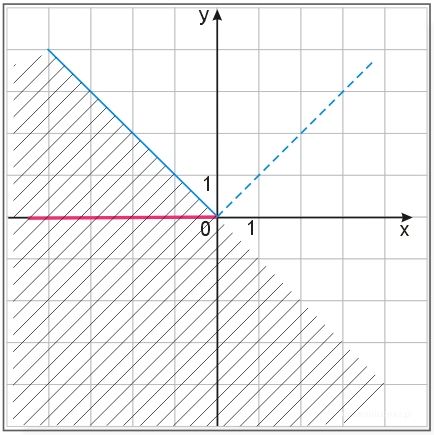
Kolorem niebieskim zaznaczono fragment wykresu funkcji \(y=|x|\) dla x mniejszych od zera. Obrazu prostej szukamy tylko w dla \(y'<-x'\)(obszar zakreskowany), a więc jest to prosta \(y=0\) tylko w zakreskowanym obszarze
Łączymy oba szkice w jeden:
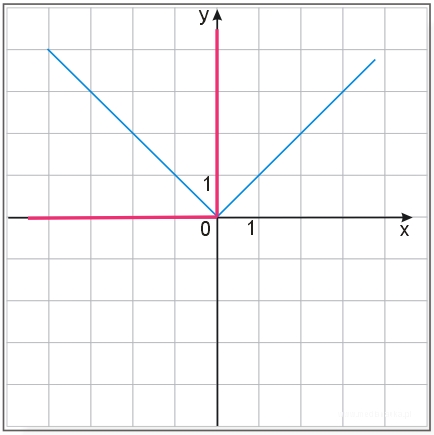
 Odpowiedź
Odpowiedź
© medianauka.pl, 2011-03-20, ZAD-1250


Zadania podobne
Zadanie nr 1.
Znaleźć obraz punktu \(P=(2,4)\) w obrocie dookoła początku układu współrzędnych o kąt \(30°\).
Zadanie nr 2.
Znaleźć obraz krzywej \(y=x^3\) w obrocie dookoła początku układu współrzędnych o kąt \(90°\).
Zadanie nr 3.
Znaleźć obraz prostej \(y=-2x+6\) w obrocie dookoła początku układu współrzędnych o kąt \(60°\).

