
Zadanie maturalne nr 13, matura 2016 (poziom rozszerzony)
Treść zadania:
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.
 Rozwiązanie zadania
Rozwiązanie zadania
Zaczniemy od sporządzenia szkicu do zadania.
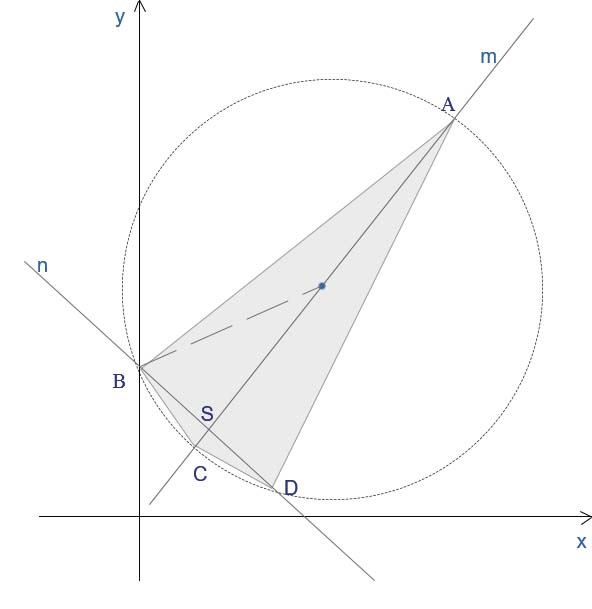
Nasza figura jest deltoidem. Musimy wyznaczyć współrzędne punktu \(C\) i \(D\). Zadanie podzielę na kilka etapów.
Etap I — Szukamy współrzędnej punktu \(D\).
Zauważamy, że punkt \(D\) leży na prostej prostopadłej do prostej \(m\), dlatego, że w deltoidzie przekątne przecinają się w punkcie \(S\) pod kątem prostym. Proste \(m\) i \(n\) są prostopadłe, a więc ich współczynniki kierunkowe są w stosunku do siebie odwrotne ze znakiem minus. Jeżeli prosta \(m\) jest opisana równaniem \(x-y+2=0\), czyli \(y=x+2\), to jej współczynnik kierunkowy jest równy \(1\). Współczynnik kierunkowy prostej \(n\) jest odwrotnością ze znakiem minus, czyli jeżeli \(n: y=ax+b\), to \(a=-1\) i \(y=-x+b\). Wiemy, że \(B=(0,8)\) leży na prostej \(n\), więc jego współrzędne spełniają nasze równie prostej:
\(y=-x+b\)
\(B=(0,8)\)
\(0=-1\cdot 0+b\)
\(b=8\)
\(a=-1\)
\(y=-x+8\)
Punkt \(S\) jest punktem przecięcia się prostych \(m\) i \(n\), czyli współrzędne punktu \(S\) są rozwiązaniem układu:
\(\begin{cases} y=x+2\\y=-x+8\end{cases}\)
\(0=2x-6\)
\(2x=6\)
\(x=3\)
\(y=3+2\)
\(y=5\)
\(S=(3,5)\)
Punkt \(S\) jest środkiem odcinka \(BD\). Współrzędne środka odcinka są średnią arytmetyczną odpowiednich współrzędnych końców odcinka. Mamy więc:
\(x_s=\frac{x_B+x_D}{2}\)
\(3=\frac{0+x_D}{2}\)
\(x_D=6\)
\(y_s=\frac{y_B+y_D}{2}\)
\(5=\frac{8+y_D}{2}\)
\(y_D=2\)
\(D=(6,2)\)
Etap II — szukamy współrzędnych punktu \(C\).
Niech środek okręgu będzie oznaczony przez \(O=(o_x,o_y)\). Wiemy, że \(O\) leży na prostej \(y=x+2\), zatem współrzędne punktu \(O=(o_x,o_x+2)\).
Ponadto wiemy, że \(|OA|=|OB|\). Długość odcinka obliczamy przez spierwiastkowanie sumy kwadratów różnicy ich współrzędnych. Jeżeli obie strony podniesiemy do kwadratu, pozbędziemy się pierwiastka i otrzymamy:
\(|OA|=|OB|\)
\(|OA|^2=|OB|^2\)
\(O=(o_x, o_y)\)
\((o_x-30)^2+(o_x+2-32)^2=(o_x-0)^2+(o_x+2-8)^2\)
\(o_x=\frac{49}{3}\)
\(o_y=o_x+2=\frac{55}{3}\)
\(O=(\frac{49}{3},\frac{55}{3})\)
Teraz już łatwo znajdziemy punkt \(C\), korzystając z tego, że punkt \(O\) jest środkiem odcinka \(AC\), a współrzędne \(A\) i \(O\) są dane:
\(o_x=\frac{x_A+x_C}{2}\)
\(\frac{49}{3}=\frac{30+x_C}{2}\)
\(\frac{98}{3}=30+x_C\)
\(x_C=\frac{8}{3}\)
\(o_y=\frac{y_A+y_C}{2}\)
\(\frac{55}{3}=\frac{32+y_C}{2}\)
\(\frac{110}{3}=32+y_C\)
\(y_C=\frac{14}{3}\)
 Odpowiedź
Odpowiedź
\(D=(6,2)\)
\( C=(\frac{8}{3}, \frac{14}{3})\)
© medianauka.pl, 2016-11-11, ZAD-3284


Zadania podobne
Zadanie nr 1.
Z dwóch listewek o długości 30 cm i 1,2 m oraz kawałka materiału zbudowano latawiec w kształcie deltoidu tak, że listewki tworzą jego przekątne. Jakie jest pole powierzchni użytego materiału?

