Usuwanie niewymierności z mianownika
Usuwanie niewymierności z mianownika wyrażenia polega na takim przekształceniu tego wyrażenia, aby w mianowniku otrzymać liczbę wymierną.
Przykłady
\(\frac{2}{\sqrt{2}}=\frac{2\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{2\sqrt{2}}{2}=\sqrt{2}\)
\(\frac{1}{\sqrt[3]{4}}=\frac{\sqrt[3]{2}}{\sqrt[3]{4}\cdot\sqrt[3]{2}}=\frac{\sqrt[3]{2}}{\sqrt[3]{8}}=\frac{\sqrt[3]{2}}{2}\)
Zatem mnożymy licznik i mianownik przez taką liczbę niewymierną, aby w mianowniku otrzymać liczbę wymierną.
Jeżeli w mianowniku mamy sumę lub różnicę korzystamy ze wzoru skróconego mnożenia: \((a+b)(a-b)=a^{2}-b^{2}\).
Przykłady
\(\frac{2}{3+\sqrt{2}}=\frac{2(3-\sqrt{2})}{(3+\sqrt{2})(3-\sqrt{2})}=\frac{6-2\sqrt{2}}{3^{2}-(\sqrt{2})^{2}}=\frac{6-2\sqrt{2}}{9-2}=\frac{6-2\sqrt{2}}{7}\)
\(\frac{1}{\sqrt{2}-\sqrt{3}}=\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}=\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2})^{2}-(\sqrt{3})^{2}}=\frac{\sqrt{2}+\sqrt{3}}{2-3}=-\sqrt{2}-\sqrt{3}\)
Podobnie postępujemy w innych przypadkach. Poniższy przykład ilustruje, jak pozbyć się niewymierności z mianownika, gdy w mianowniku mamy do czynienia z sumą trzech liczb niewymiernych.
Przykłady
Usuń niewymierność z mianownika liczby \(\frac{1}{\sqrt{2}+\sqrt{3}+\sqrt{5}}\).
Tutaj również można zastosować wzór skróconego mnożenia, jednak dla ułatwienia sobie rachunków można dokonać podstawienia \(m=\sqrt{2}+\sqrt{3}\).
Mamy wówczas:
\(\frac{1}{\sqrt{2}+\sqrt{3}+\sqrt{5}}=\frac{1}{m+\sqrt{5}}=\frac{m-\sqrt{5}}{(m+\sqrt{5})(m-\sqrt{5})}=\frac{m-\sqrt{5}}{m^{2}-5}\)
Podstawiając teraz z powrotem za \(m\) liczbę \(\sqrt{2}+\sqrt{3}\), możemy kontynuować rachunki:
\(\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{(\sqrt{2}+\sqrt{3})^{2}-5}=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{(2+2\sqrt{2}\sqrt{3}+3)-5}=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{2\sqrt{6}+5-5}=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{2\sqrt{6}}=\)
\(\frac{(\sqrt{2}+\sqrt{3}-\sqrt{5})\cdot\sqrt{6}}{2\sqrt{6}\cdot\sqrt{6}}=\frac{\sqrt{12}+\sqrt{18}-\sqrt{30}}{2\cdot6}=\frac{2\sqrt{3}+3\sqrt{2}-\sqrt{30}}{12}\)
Pytania
Po co usuwać niewymierność z mianownika?
Niewymierność z mianownika ułamka usuwa się z co najmniej dwóch powodów:
- dla możliwości uzyskania lepszej dokładności przybliżenia wartości ułamka (dzieląc na przykład kolejne przybliżenia pierwiastka z dwóch przez 2, uzyskujemy dokładniejsze wyniki, niż dzieląc jedność przez kolejne przybliżenia pierwiastka z dwóch),
- dla łatwego ręcznego obliczenia przybliżenia wartości ułamka z niewymiernością (łatwiej jest podzielić przybliżenie przez liczbę naturalną niż odwrotnie).
Zadania z rozwiązaniami

Zadanie nr 1.
Uprościć wyrażenie \(W=\frac{1}{\sqrt{x+1}}-\frac{\sqrt{x-1}}{\sqrt{x+1}}+\frac{\sqrt{x^2-1}}{x+1}\), wiedząc, że \(x>-1\).

Zadanie nr 2.
Pozbyć się niewymierności z mianownika
a) \(\frac{7}{1-\sqrt{7}}\)
b) \(\frac{1}{\sqrt{2}+\sqrt{3}+\sqrt{5}}\)
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-02-15, A-148
Data aktualizacji artykułu: 2023-03-23

 Pierwiastek arytmetyczny
Pierwiastek arytmetyczny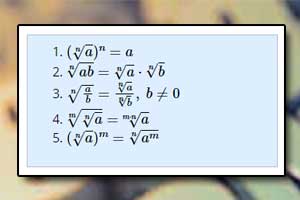 Działania na pierwiastkach
Działania na pierwiastkach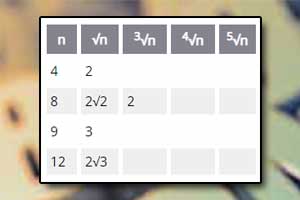 Wyłączanie czynnika przed pierwiastek
Wyłączanie czynnika przed pierwiastek