Pochodne cząstkowe
Dana jest funkcja wielu zmiennych \(y=f(x_1, x_2, x_3, ..., x_n)\) określona w pewnym otoczeniu punktu \(p_0=(x_{01}, x_{02}, x_{03}, ..., x_{0n})\).
Pochodna cząstkowa funkcji \(f\) względem zmiennej \(x_i\) jest zdefiniowana jako granica ilorazu różnicowego:
Opis: \(x_i\) jest tutaj uważana za zmienną, względem której obliczamy powyższą granicę, a wszystkie pozostałe \(n-1\) zmiennych należy traktować jako parametry (stałe).
Z powyższej definicji widać, że jeżeli mamy funkcję n zmiennych, możemy dla niej obliczyć \(n\) pochodnych cząstkowych.
Pochodne wyższych rzędów oblicza się poprzez różniczkowanie znów po dowolnych zmiennych. Pochodne wyższych rzędów obliczane względem zmiennych różnych niż wybrana początkowo to tak zwane pochodne cząstkowe mieszane.
Oznaczenia pochodnej cząstkowej
Dla pochodnej cząstkowej względem x możemy stosować następujące oznaczenia:
\(\frac{\partial f}{\partial x}, f_x, f'_x, \partial_xf\)
Dla pochodnej mieszanej używamy symbolu:
\(\frac{\partial^2 f}{\partial x\partial y}\)
Jak obliczać pochodne cząstkowe?
Aby obliczyć pochodną cząstkową, możemy stosować wszystkie wzory na pochodną z rachunku różniczkowego jednej zmiennej.
Przykład 1
Obliczyć pochodne cząstkowe względem zmiennych \(x, y,z\) funkcji \(f(x,y,z)=x^2y^3z^4\).
Rozwiązanie:
\(\frac{\partial f}{\partial x}=2xy^3z^4\)
\(\frac{\partial f}{\partial y}=x^23y^2z^4\)
\(\frac{\partial f}{\partial z}=x^2y^34z^3\)
Przykład 2
Dana jest funkcja \(f(x,y)=x^2y^3\). Obliczyć: \(\frac{\partial^2 f}{\partial x\partial y}\).
Rozwiązanie:
\(\frac{\partial^2 f}{\partial x \partial y}=\frac{\partial f}{\partial x } (x^2\cdot3y^2)=2x\cdot3y^2=6xy^2\)
Rząd pochodnej cząstkowej
Liczbę zastosowanych różniczkowań to tak zwany rząd pochodnej cząstkowej.
Powiązane materiały
© medianauka.pl, 2021-08-22, A-4148
Data aktualizacji artykułu: 2023-05-17

 Pochodna funkcji
Pochodna funkcji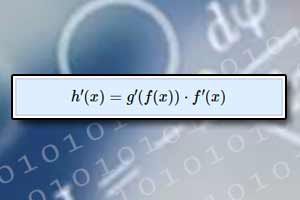 Pochodna funkcji złożonej
Pochodna funkcji złożonej Pochodna drugiego rzędu i dalsze pochodne
Pochodna drugiego rzędu i dalsze pochodne Pochodna funkcji
Pochodna funkcji