Pochodna drugiego rzędu i dalsze pochodne

Definicja

Jeżeli funkcja ma pochodną, to nazywamy ją drugą pochodną lub pochodną drugiego rzędu i oznaczamy symbolem:

Przykład

Aby obliczyć drugą pochodną funkcji, obliczamy najpierw jej pochodną, a potem obliczamy pochodną otrzymanego wyniku.

$f(x)=x, \ f'(x)=(x)'=1,\ f''(x)=(1)'=0\\f(x)=\sin{x}, \ f'(x)=\cos{x},\ f''(x)=-\sin{x}\\f(x)=x^2+1, \ f'(x)=2x,\ f''(x)=2$

Pochodne wyższych rzędów

W analogiczny sposób określamy pochodne wyższych rzędów. Oznaczamy je kolejno za pomocą liczb rzymskich:

$f^{II},f^{III},f^{IV},f^{V},...$

lub za pomocą liczb arabskich, ujmując je w nawiasy: $f^{II},f^{(3)},f^{(4)},f^{(5)},...$

Przykład

Obliczmy pochodną piątego rzędu funkcji $f(x)=x^{10}$ .

$f(x)=x^{10}\\f'(x)=10x^9\\f^{II}(x)=90x^8\\f^{III}(x)=720x^7\\f^{IV}(x)=5040x^6\\f^{V}(x)=30240x^5$

Zadania związane z tematem:
Pochodna drugiego rzędu i dalsze pochodne

Zadanie - pochodna drugiego rzędu
Obliczyć drugą pochodną funkcji:
a) $f(x)=\sqrt{x}$
b) $f(x)=x^2-x^3+\frac{1}{x^3}$

Zadanie - pochodna drugiego rzędu
Obliczyć drugą pochodną funkcji:
a) $f(x)=\cos^2{2x}$
b) $f(x)=\frac{x^2+1}{x^2-1}$

Zadanie - druga pochodna funkcji
Dla jakiej wartości argumentu x druga pochodna funkcji $f(x)=\frac{1}{1+x}$ jest równa $\frac{1}{4}$ ?

Zadanie - druga pochodna funkcji
Rozwiąż równanie , gdzie y=x³+1.

Pochodna funkcji

Co to jest pochodna funkcji, pochodna funkcji w punkcie, iloraz różnicowy?

Obliczanie pochodnych

Wzory na pochodne funkcji elementarnych, obliczanie pochodnych, zadania i przykłady

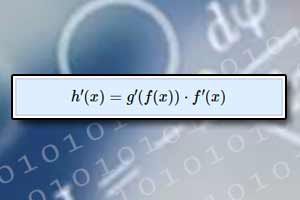Pochodna funkcji złożonej

Złożenie funkcji - omówienie zagadnienia wraz z animacją prezentującą przykład obliczania pochodnej funkcji złożonej.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.