Średnia ważona
Jak obliczyć średnią ważoną i kiedy ma ona zastosowanie? Zacznijmy od definicji.
Definicja
Średnia ważona liczb rzeczywistych \(x_1,x_2,...,x_n\) z odpowiadającymi im odpowiednio wagami dodatnimi\(w_1,w_2,...,w_n\) jest to liczba \(\overline{x_w}\) określona wzorem:
Kiedy stosujemy średnią ważoną?
Średniej ważonej używamy wówczas, kiedy opracowując dane statystyczne chcemy scharakteryzować pewien cały ich zestaw i dodatkowo pewne dane mają większe znaczenie od innych. Znaczenie określają właśnie wagi.
Przykłady
Powyższy wzór na średnią ważoną zastosujemy w zadaniu:
Jasiek ma z matematyki następujące oceny: 3+ (klasówka), 2+(klasówka), 5, 5, 4, a Paweł: 4 (klasówka), 4+ (klasówka), 1, 3, 2. Kto jest lepszym uczniem, zakładając że waga ocen z klasówek jest równa 0.6, a pozostałych 0.4?
O tym, czy uczeń jest dobry, bardzo dobry czy słaby decydują między innymi oceny. Musimy jednak wystawić uczniowi jedną ocenę, która go scharakteryzuje. Mamy określone wagi, więc obliczymy średnią ważoną ocen. Mamy 5 ocen, plusy traktujemy jako liczbę 0.5.
\(\overline{x}_{Jan}=\frac{3,5\cdot 0,6+2,5\cdot 0,6+5\cdot 0,4+5\cdot 0,4+4\cdot 0,4}{0,6+0,6+0,4+0,4+0,4}=\frac{9,2}{2,4}=3,8(3)\)
\(\overline{x}_{Paweł}=\frac{4\cdot 0,6+4,5\cdot 0,6+1\cdot 0,4+3\cdot 0,4+2\cdot 0,4}{0,6+0,6+0,4+0,4+0,4}=\frac{7,5}{2,4}=3,125\)
Możemy stwierdzić, że Jasiek jest lepszym uczniem od Pawła.
Pytania
Jak się liczy średnią ważoną?
Pokazaliśmy to wyżej, jednak użyjemy prostszego przykładu. Jeżeli otrzymałeś 3 punty w grze na poziomie trudnym (poziom 1) i 4 punkty na poziomie dwa razy łatwiejszym (poziom 2), to jak policzyć średnią? Przypiszmy wagę 2 poziomowi 1 i wagę 1 poziomowi 2. Obliczmy teraz średnią ważoną: \(\overline{x}=\frac{(3\cdot 2+4\cdot 1)}{(2+1)}=\frac{10}{3}=3,33...\)
Czy wagi mogą być ujemne?
Zgodnie z definicją średniej ważonej wagi są dodatnie.
Jak się liczy średnią ważoną ocen?
Spójrz na przykład w naszym artykule.
Jak obliczyć średnią ważoną w programie Excel?
W programie Excel nie ma wbudowanej funkcji do obliczania średniej ważonej. Trzeba napisać własną formułę. Proponuję dla przykładu w jednej kolumnie (komórki A2 do A3) napisać liczby 3 i 2 (liczba i jej waga), w drugiej kolumnie (komórki B2 do B3) liczby 4 i 1 (liczba i jej waga), a następnie użyć funkcji SUMA.ILOCZYNÓW i SUMA, poprzez wpisanie formuły '=SUMA.ILOCZYNÓW(A2:B2;A3:B3)/SUMA(A3:B3)' w kolejnym wierszu.
Inne zagadnienia z tej lekcji
© medianauka.pl, 2011-08-13, A-1420
Data aktualizacji artykułu: 2023-07-24

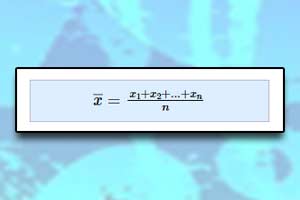 Średnia arytmetyczna
Średnia arytmetyczna Mediana
Mediana Dominanta
Dominanta Wariancja i odchylenie standardowe
Wariancja i odchylenie standardowe