Zadanie — objętość sześcianu, zadanie z treścią

Treść zadania:

Rozwiązanie zadania

Zakładamy, że kulki wrzucane do urny układają się ściśle obok siebie i jedna na drugiej. Kulka taka zajmuje część przestrzeni zawartą w sześcianie o krawędziach \(1\ cm\ x\ 1cm\ x\ 1\ cm\), czyli o objętości \(V_k=1\ cm^3\) (na tę objętość przypada objętość kulki i pustej przestrzeni między kulkami). Cała urna ma wymiary \(100\ cm\ x\ 100\ cm\ x\ 100\ cm\) (bo jeden metr jest równy 100 cm), więc objętość urny jest równa:

\(V=a^3=(100\ cm)^3=1000000\ cm^3\)

Ile mieści się w przestrzeni urny objętości kulek? Liczbę tę znajdziemy dzieląc objętość urny przez objętość przestrzeni zajmowaną przez kulkę.

\(\frac{V}{V_k}=\frac{1000000\ cm^3}{1\ cm^3}=1000000\)

Zadanie to można rozwiązać także nie używając pojęcia objętości. Mianowicie w długości 1 m mieści się 100 kulek (1 rząd)), na dnie urny zmieści się 100 rzędów. To już 100x100=10 000 kulek. Warstw w urnie zmieści się również 100, czyli 100 x 10 000=1000 000.

Odpowiedź

© medianauka.pl, 2011-10-18, ZAD-1495

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

Przekątna sześcianu ma długość równą \(\sqrt{3}\). Oblicz objętość tego sześcianu.

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

Przekątna sześcianu ma długość \(4\sqrt{3}\). Pole powierzchni tego sześcianu jest równe

A. 96

B. \(24\sqrt{3}\)

C. 192

D. \(16\sqrt{3}\)

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Dany jest sześcian \(ABCDEFG\) o krawędzi długości \(a\). Punkty \(E, F, G, B\) są wierzchołkami ostrosłupa \(EFGB\) (zobacz rysunek).

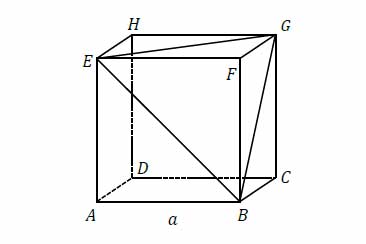
Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe

A. \(a^2\)

B. \(\frac{3\sqrt{3}}{2}\cdot a^2\)

C. \(\frac{3}{2}\cdot a^2\)

D. \(\frac{3+\sqrt{3}}{2}\cdot a^2\)

Pokaż rozwiązanie zadania.

Zadanie nr 4 — maturalne.

Dany jest sześcian \(ABCDEFGH\) o krawędzi długości 6. Punkt \(S\) jest punktem przecięcia przekątnych \(AH\) i \(DE\) ściany bocznej \(ADHE\) (zobacz rysunek).

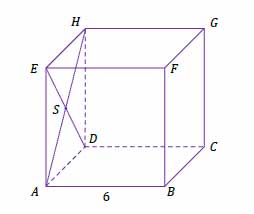
Oblicz wysokość trójkąta \(SBH\) poprowadzoną z punktu \(S\) na bok \(BH\) tego trójkąta. Zapisz obliczenia.

Pokaż rozwiązanie zadania.