Nauka » Matematyka » Układ nierówności

Zadanie - układ nierówności z dwomia niewiadomymi

Dany jest układ nierówności
$\begin{cases}x>-1 \\ x<1 \\y>-1\\ y<1 \end{cases}$
Który z punktów:
A(0,0),
B(1,1),
C(0,-1),
należy do graficznego rozwiązania układu nierówności?

Rozwiązanie zadania uproszczone

Punkty B i C leżą na brzegu kwadratu, który nie należy do rozwiązania układu.
Układ równań spełnia tylko punkt A

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Podstawiamy współrzędne każdego z punktów za zmienne x oraz y do układu nierówności i sprawdzamy, czy spełnione są wszystkie nierówności.

Punkt A(0,0)=(x,y)

$\begin{cases}0>-1 \\ 0<1 \\0>-1\\ 0<1 \end{cases}$

Wszystkie nierówności są prawdziwe, a więc punkt A spełnia układ równań

Punkt B(1,1)=(x,y)

$\begin{cases}1>-1 \\ 1<1 \\1>-1\\ 1<1 \end{cases}$

Druga i czwarta nierówność jest fałszywa, a więc punkt B nie należy do graficznego rozwiązania układu równań

Punkt C(0,-1)=(x,y)

$\begin{cases}0>-1 \\ 0<1 \\-1>-1\\ -1<1 \end{cases}$

Trzecia nierówność jest fałszywa, a więc punkt C nie należy do graficznego rozwiązania układu równań

Zadanie można też rozwiązać graficznie. Należy sporządzić wykres układu i sprawdzić, czy punkty A, B i C należą do wykresu układu nierówności

Punkty B i C leżą na brzegu kwadratu, który nie należy do rozwiązania układu.

Odpowiedź

Układ równań spełnia tylko punkt A

Zadania podobne

Zadanie - układ nierówności z dwiema niewiadomymi
Rozwiązać graficznie układ nierówności
$\begin{cases}y<3x+1 \\ y<-3x+1 \\y>x-1 \end{cases}$

Pokaż rozwiązanie zadania

Zadanie - układ nierówności liniowych z dwiema niewiadomymi
Opisać za pomocą wzoru zbiór przedstawiony na rysunku, wiedząc, że punkty A, B i C mają całkowite współrzędne.
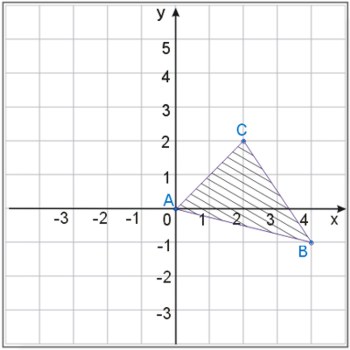
Układ nierówności graficznie

Pokaż rozwiązanie zadania

Zadanie - układ nierówności z dwiema niewiadomymi
Rozwiązać graficznie układ nierówności:
$\begin{cases} x-y<1 \\ x+y\geq 1 \end{cases}$

Pokaż rozwiązanie zadania

Zadanie - układ nierówności z dwiema niewiadomymi
Rozwiązać układ nierówności:
$\begin{cases} \ \ 2y+x<1 \\ -2y-x<-2 \end{cases}$

Pokaż rozwiązanie zadania