Zadanie - układ nierówności z dwiema niewiadomymi
Treść zadania:
Rozwiązać układ nierówności:
\(\begin{cases}2y+x<1\\-2y-x<-2 \end{cases}\)
Rozwiązanie zadania
Dodamy stronami do siebie obie nierówności:
\(\underline{_+\begin{cases}\ \ 2y+x<1\\-2y-x<-2 \end{cases}}\)
\( \ \ \ \ \ \ \ \ \ \ \ \ \ 0<-1\)
Otrzymaliśmy nierówność nieprawdziwą. Stąd wniosek, że układ nierówności jest sprzeczny. Sprawdźmy rozwiązanie graficzne, w tym celu w obu nierównościach wyznaczamy \(y\).
\(\begin{cases}\ \ 2y<-x+1/:2\\-2y<x-2/:(-2)\end{cases}\)
\(\begin{cases}y<-\frac{1}{2}x+\frac{1}{2}\\y>-\frac{1}{2}x+1 \end{cases}\)
W jednym układzie współrzędnych sporządzamy wykresy funkcji \(y=-\frac{1}{2}x+\frac{1}{2}, \ y=-\frac{1}{2}x+1\) i zaznaczamy odpowiednie obszary.
Widzimy, że zakreskowane obszary nie mają części wspólnych, zatem układ nierówności nie ma rozwiązania.
© medianauka.pl, 2010-02-20, ZAD-631


Zadania podobne
Zadanie nr 1.
Rozwiązać graficznie układ nierówności
\(\begin{cases}y<3x+1 \\ y<-3x+1 \\y>x-1 \end{cases}\)
Zadanie nr 2.
Dany jest układ nierówności
\(\begin{cases}x>-1 \\ x<1 \\y>-1\\ y<1 \end{cases}\)
Który z punktów: \(A(0,0), B(1,1), C(0,-1)\) należy do graficznego rozwiązania układu nierówności?
Zadanie nr 3.
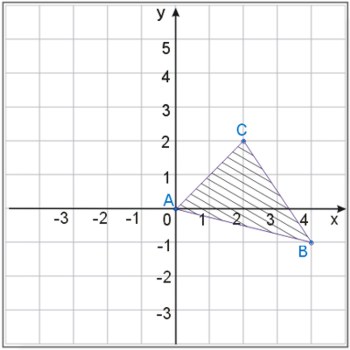
Opisać za pomocą wzoru zbiór przedstawiony na rysunku, wiedząc, że punkty A, B i C mają całkowite współrzędne.
Zadanie nr 4.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x-y<1 \\ x+y\geq 1 \end{cases}\)

