Zadanie - układ nierówności z dwiema niewiadomymi
Treść zadania:
Rozwiązać graficznie układ nierówności
\(\begin{cases}y<3x+1 \\ y<-3x+1 \\y>x-1 \end{cases}\)
 Rozwiązanie zadania
Rozwiązanie zadania
Rozwiążemy ten układ etapami.
Etap 1
Wykreślamy wykres nierówności \(y<3x+1\). W tym celu sporządzamy najpierw wykres prostej \(y=3x+1\). Sporządzamy tabelkę zmienności funkcji (wystarczą 2 punkty):
| \(x\) | 0 | 1 |
| \(y=3x+1\) | 1 | 4 |
Zaznaczamy linią przerywaną prostą i zakreślamy obszar wszystkich wartości mniejszych od wartości funkcji \(y=3x+1\) (wszystkie punkty leżące poniżej punktów na wykresie).
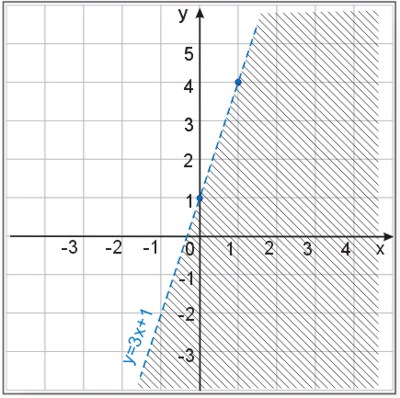
Pole zakreskowane, bez prostej jest rozwiązaniem pierwszej nierówności.
Etap 2
Wykreślamy wykres nierówności \(y<-3x+1\) w tym samym układzie współrzędnych. W tym celu sporządzamy wykres prostej \(y=-3x+1\). Sporządzamy tabelkę zmienności funkcji:
| \(x\) | 0 | 1 |
| \(y=-3x+1\) | 1 | -2 |
Zaznaczamy linią przerywaną prostą i zakreślamy obszar wszystkich wartości mniejszych od wartości funkcji \(y=-3x+1\) (wszystkie punkty leżące poniżej punktów na wykresie).
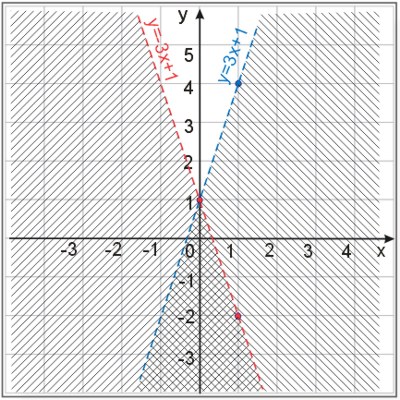
Pole zakreskowane, bez prostej jest rozwiązaniem drugiej nierówności. Pole podwójnie zakreskowane jest rozwiązaniem układu tych dwóch nierówności.
Etap 3
Wykreślamy wykres nierówności \(y>x+1\) w tym samym układzie współrzędnych. W tym celu sporządzamy wykres prostej \(y=x-1\). Sporządzamy tabelkę zmienności funkcji:
| \(x\) | 0 | 1 |
| \(y=x-1\) | -1 | 0 |
Zaznaczamy linią przerywaną prostą i zakreślamy obszar wszystkich wartości większych od wartości funkcji \(y=x-1\) (wszystkie punkty leżące powyżej punktów na wykresie).
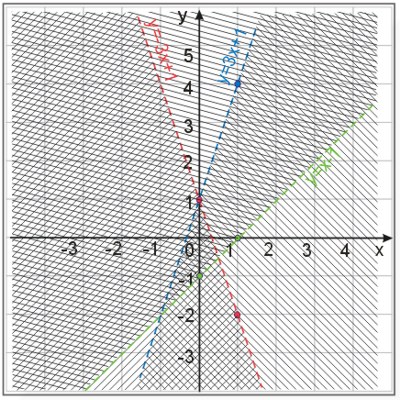
Pole zakreskowane, bez prostej jest rozwiązaniem trzeciej nierówności. Pole potrójnie zakreskowane jest rozwiązaniem układu trzech nierówności.
 Odpowiedź
Odpowiedź
Rozwiązaniem układu nierówności jest pole zakreskowanej figury bez brzegu:
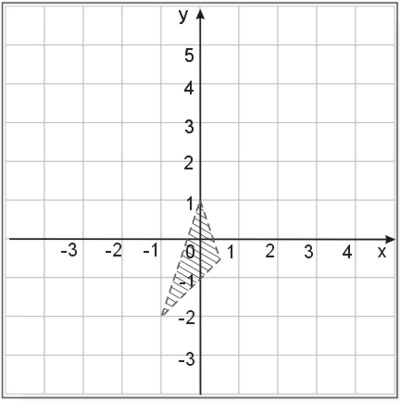
© medianauka.pl, 2010-02-14, ZAD-627


Zadania podobne
Zadanie nr 1.
Dany jest układ nierówności
\(\begin{cases}x>-1 \\ x<1 \\y>-1\\ y<1 \end{cases}\)
Który z punktów: \(A(0,0), B(1,1), C(0,-1)\) należy do graficznego rozwiązania układu nierówności?
Zadanie nr 2.
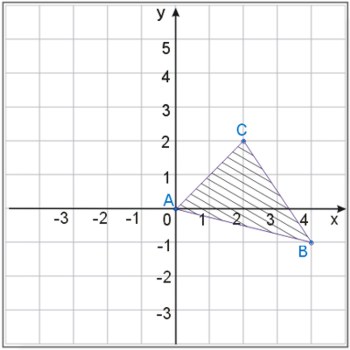
Opisać za pomocą wzoru zbiór przedstawiony na rysunku, wiedząc, że punkty A, B i C mają całkowite współrzędne.
Zadanie nr 3.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x-y<1 \\ x+y\geq 1 \end{cases}\)
Zadanie nr 4.
Rozwiązać układ nierówności:
\(\begin{cases}2y+x<1\\-2y-x<-2 \end{cases}\)

