Moment bezwładności

Miarą bezwładności ciała w ruchu obrotowym jest moment bezwładności.

Moment bezwładności bryły względem danej osi nazywamy sumę iloczynu mas poszczególnych punktów bryły i kwadratów odległości od danej osi.

\(I=\sum_{i=1}^{n}\quad m_ir_i^2=m_1r_1^2+m_2r_2^2+...+m_nr_n^2\)

Zwykle jednak mamy do czynienia z bryłami o ciągłym rozkładzie masy, trudno wówczas zastosować powyższy wzór.

Poziom zaawansowany

Sumowanie w powyższym wzorze można zastąpić całkowaniem. Otrzymamy wówczas bardziej użyteczną zależność:

\(I=\int{r^2dm}\)

Aby z niej skorzystać musimy znać rozkład masy w zależności od \(r\). wówczas całkujemy taką funkcję po dm, otrzymując moment bezwładności danej bryły.

Dla każdej bryły moment bezwładności może być inny. Nawet dla tej samej bryły, ale różnych osi obrotów moment bezwładności jest różny.

Poniższa tabela zawiera wzory na momenty bezwładności dla różnych brył.

Tablica bezwładności brył sztywnych

Bryła	Oś	Moment bezwładności
Kula jednorodna o promieniu \(R\)	Oś, która przechodzi przez środek kuli	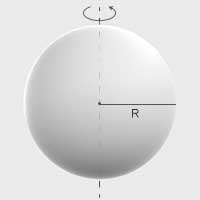\(I=\frac{2}{5}mR^2\)
Cienka powłoka sferyczna o promieniu \(R\)	Oś, która przechodzi przez środek sfery	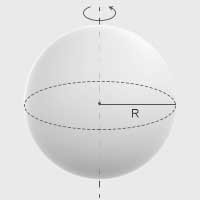\(I=\frac{2}{3}mR^2\)
Jednorodny, pełny walec o promieniu podstawy \(R\)	Podłużna oś symetrii	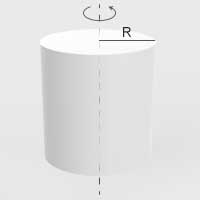\(I=\frac{1}{2}mR^2\)
Wydrążony walec o promieniu wewnętrznym \(R_w\) i zewnętrznym \(R_z\)	Podłużna oś symetrii	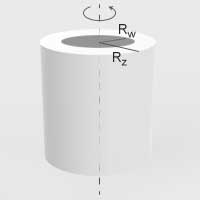\(I=\frac{1}{2}m(R_w^2+R_z^2)\)
Walec o promieniu wewnętrznym podstawy \(R\) i wysokości \(H\)	Oś prostopadła do osi podłużnej symetrii, przechodząca przez środek walca	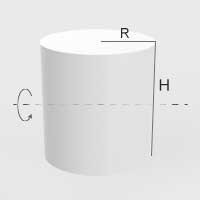\(I=\frac{1}{12}m(H^2+3R^2)\)
Pręt o długości \(l_\)	Oś prostopadła do pręta, przechodząca przez jego początek	\(I=\frac{1}{3}ml^2\)
Pręt o długości \(l\)	Oś prostopadła do pręta, przechodząca przez jego środek	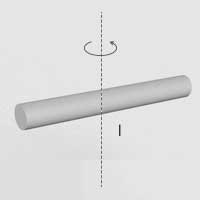\(I=\frac{1}{12}ml^2\)
Pręt o długości \(l_\)	Oś przechodząca przez jego środek nachylona do niego pod kątem alfa	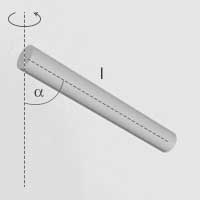\(I=\frac{1}{3}ml^2\sin^2\alpha\)
Obręcz cienkościenna o promieniu \(R\)	Oś prostopadła do płaszczyzny obręczy, przechodząca przez jej środek	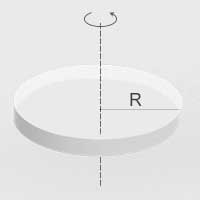\(I=mR^2\)
Obręcz cienkościenna o promieniu \(R\)	Oś leżąca w płaszczyźnie obręczy, przechodząca przez jej środek	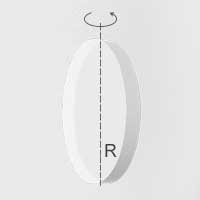\(I=\frac{1}{2}mR^2\)
Cienka tarcza o promieniu \(R\)	Oś prostopadła do płaszczyzny tarczy, przechodząca przez jej środek	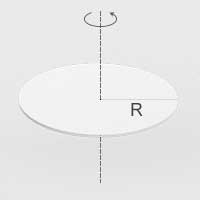\(I=\frac{1}{2}mR^2\)
Stożek o promieniu podstawy \(R\)	Oś prostopadła do płaszczyzny podstawy, przechodząca przez wierzchołek stożka	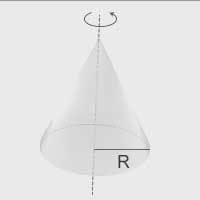\(I=\frac{3}{10}mR^2\)
Prostopadłościan o krawędziach \(a\]), \(b\) i \(c\)	Oś prostopadła do podstawy o bokach a i b, przechodząca przez punkt przecięcia się przekątnych podstawy	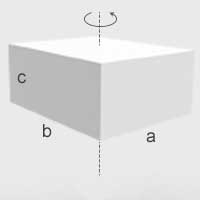\(I=\frac{1}{12}m(a^2+b^2)\)
Sześcian o krawędzi \(a\)	Oś prostopadła do podstawy, przechodząca przez środek podstawy	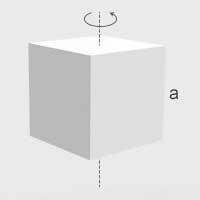\(I=\frac{1}{6}ma^2\)