Twierdzenie Steinera

Twierdzenie Steinera brzmi:

Moment bezwładności I bryły względem dowolnej osi jest równy sumie momentu bezwładności I₀ względem osi równoległej, przechodzącej przez środek masy bryły oraz iloczynu masy tej bryły i kwadratu odległości d obu osi.

Dzięki temu twierdzeniu możemy, znając moment bezwładności bryły względem osi przechodzącej przez środek masy bryły, obliczyć moment bezwładności według każdej osi równoległej.

Przykład

Aby obliczyć moment bezwładności kuli o masie 1 kg i promieniu 10 cm względem osi stycznej do tej kuli możemy zastosować twierdzenie Steinera.

Twierdzenie Steinera

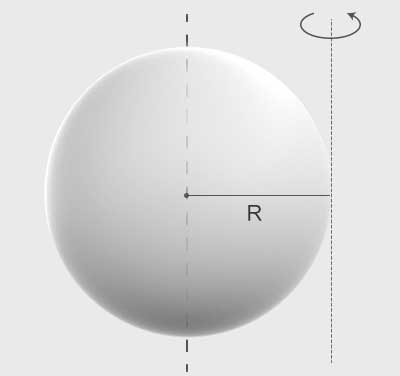
Znamy wzór na moment bezwładności kuli względem osi symetrii (zobacz tablicę). Wzór jest następujący:

$I=\frac{2}{5}mR^2$

Odległość obu osi od siebie wynosi R. Zgodnie z twierdzeniem Steinera mamy:

$I=I_0+md^2=\frac{2}{5}mR^2+mR^2=\frac{7}{5}mR^2=\\=\frac{7}{5}\cdot 1 kg\cdot(0,1m)^2=\frac{7}{500}kg\cdot m^2$

Inne zagadnienia z tej lekcji

Dynamika ruchu po okręgu

Bryła sztywna

Rodzaje ruchu bryły sztywnej

Moment siły

Moment bezwładności

Pierwsza zasada dynamiki ruchu obrotowego

Druga zasada dynamiki dla ruchu obrotowego

Trzecia zasada dynamiki dla ruchu obrotowego

Moment pędu

Ruch obrotowy - wzory