Moment pędu

Zapamiętaj

Moment pędu - wzory

$\vec{L}=\vec{r}\times{\vec{p}}=m\vec{r}\times{\vec{v}}$

$\vec{L}=I\vec{\omega}$

Moment pędu albo inaczej kręt określamy nieco inaczej dla punktu materialnego, który porusza się ruchem po okręgu i inaczej dla bryły sztywnej, która porusza się ruchem obrotowym.

Moment pędu punktu materialnego

Moment pędu punktu materialnego względem punktu O osi obrotu jest to iloczyn wektorowy wektora wodzącego $\vec{r}$ i pędu $\vec{p}$ tego punktu. Początek wektora $\vec{r}$ leży w punkcie O.

$\vec{L}=\vec{r}\times{\vec{p}}=m\vec{r}\times{\vec{v}}$

gdzie:

$\vec{L}$ - moment pędu;

$\vec{r}$ - promień wodzący;

$\vec{p}$ - pęd punktu materialnego;

m - masa punktu materialnego;

$\vec{v}$ - prędkość punktu materialnego.

Warto zauważyć, że wektor momentu pędu jest prostopadły jednocześnie do wektora wodzącego i do wektora pędu lub prędkości punktu materialnego. Oznacza to, że wektor momentu pędu nie leży w płaszczyźnie wymienionych wyżej wektorów (spójrz na poniższy rysunek).

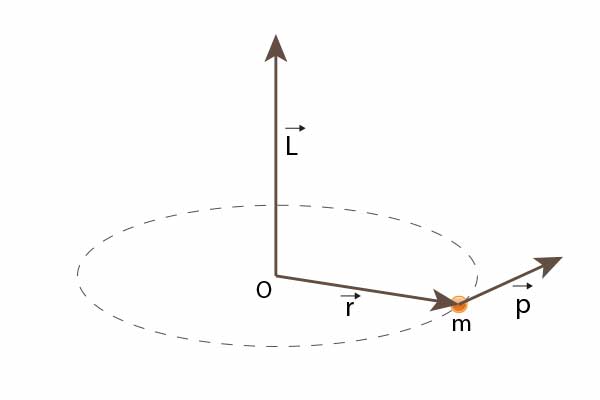
moment pędu

Zwrot wektora momentu pędu określa reguła śruby prawoskrętnej.

Jak wyliczyć wartość momentu pędu? Korzystamy z definicji iloczynu wektorowego:

Moment pędu bryły sztywnej

Moment pędu bryły sztywnej względem osi symetrii tej bryły wyraża się wzorem.

$\vec{L}=I\vec{\omega}$

gdzie:

$\vec{L}$ - moment pędu;

I - moment bezwładności;

$\vec{\omega}$ - prędkość kątowa.

Warto zauważyć, że kierunek i zwrot momentu pędu jest zgodny z kierunkiem i zwrotem wektora prędkości kątowej.

Inne zagadnienia z tej lekcji

Dynamika ruchu po okręgu

Na ciało doznające przyspieszenia dośrodkowego działa siła o stałej wartości i zwrócona do środka okręgu. Jest to siła dośrodkowa. W nieinercjalnym układzie odniesienia pojawia się szczególny przypadek siły bezwładności - siła odśrodkowa bezwładności.

Bryła sztywna

co to jest bryła sztywna? Bryła sztywna jest to ciało fizyczne, które pod wpływem działania sił zewnętrznych nie ulega odkształceniom. Jest to jedynie pojęcie modelowe. W rzeczywistości nie ma idealnej bryły sztywnej. Dla bryły sztywnej wnioski i zależności są słuszne jak dla układu punktów materialnych.

Rodzaje ruchu bryły sztywnej

Rodzaje ruchu bryły sztywnej. Bryła sztywna z uwagi na to, iż jest rozciągła w przestrzeni, może poruszać się ruchem postępowym i obrotowym. Co to jest ruch postępowy? Co to jest ruch obrotowy brył sztywnej? Ilustracja ruchu postępowego i obrotowego.

Moment siły

Moment siły F względem punktu O osi obrotu jest to iloczyn wektorowy wektora wodzącego r punktu przyłożenia siły F i tej siły. Początek wektora r leży w punkcie O. Moment siły jest też nazywany inaczej momentem obrotowym, a wektor wodzący ramieniem siły. Jednostką momentu siły jest niutonometr.

Moment bezwładności

Definicja momentu bezwładności oraz tablica momentów bezwładności dla różnych brył. Moment bezwładności bryły względem danej osi nazywamy sumę iloczynu mas poszczególnych punktów bryły i kwadratów odległości od danej osi. Dla każdej bryły moment bezwładności może być inny.

Twierdzenie Steinera

Twierdzenie Steinera wraz z przykładem. Moment bezwładności I bryły względem dowolnej osi jest równy sumie momentu bezwładności I0 względem osi równoległej, przechodzącej przez środek masy bryły oraz iloczynu masy tej bryły i kwadratu odległości d obu osi.

Pierwsza zasada dynamiki ruchu obrotowego

Pierwsza zasada dynamiki ruchu obrotowego. Jeżeli na bryłę sztywną nie działają żadne momenty sił, to bryła ta pozostaje nieruchoma lub wykonuje ruch obrotowy jednostajny (ze stałą prędkością kątową).

Druga zasada dynamiki dla ruchu obrotowego

Druga zasada dynamiki dla ruchu obrotowego. Jeżeli wypadkowy moment sił, które działają na bryłę nie jest równy zeru, to bryła porusza się ruchem zmiennym obrotowym z przyspieszeniem kątowym, które jest wprost proporcjonalne do wypadkowego momentu sił.

Trzecia zasada dynamiki dla ruchu obrotowego

Trzecią zasadę dynamiki dla ruchu obrotowego można określić w następujący sposób: Jeżeli na bryłę A działa bryła B pewnym momentem siły, to bryła B działa na bryłę A momentem równym co do wartości, ale przeciwnie skierowanym.

Ruch obrotowy - wzory

W niniejszym artykule zestawiono najważniejsze wzory i oznaczenia związane z ruchem obrotowym. W tabeli opisano oprócz wielkości związanych z ruchem obrotowym ich odpowiedniki w ruchu prostoliniowym.