Koniunkcja
Co to jest koniunkcja albo iloczyn logiczny?
Niech p i q oznaczają zdania logiczne.
Przykłady
W poniższej tabeli znajdują się przykłady iloczynu logicznego.
| p | q | p ∧ q | wartość logiczna p ∧ q |
|---|---|---|---|
| 5 jest liczbą nieparzystą. (zdanie prawdziwe) |
5 jest liczbą pierwszą. (zdanie prawdziwe) |
5 jest liczbą pierwszą i nieparzystą. | Prawda |
(zdanie prawdziwe) |
(zdanie fałszywe) |
Fałsz | |
| Słońce jest planetą. (zdanie fałszywe) |
Słońce jest pięć razy większe od Jowisza. (zdanie fałszywe) |
Słońce jest planetą i jest pięć razy większe od Jowisza. | Fałsz |
Wyniki iloczynu logicznego dla zdań p i q, gdy p i q przybierają różne wartości logiczne, ilustruje poniższa tabela:
| p | q | p ∧ q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Zatem koniunkcja dowolnych zdań p i q jest prawdziwa tylko w przypadku, gdy oba zdania p i q są prawdziwe.
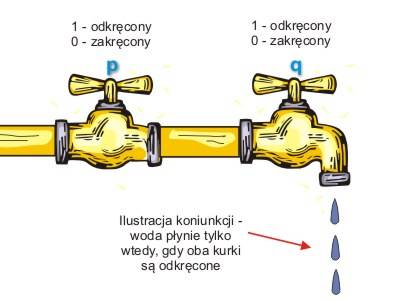
Zawór koniunkcji
Jak zapamiętać wyniki koniunkcji? Można wyobrazić sobie rurę, przez którą przepływa woda. W rurze znajdują się obok siebie dwa kurki: p i q. Stan kurka „odkręcony” niech oznacza wartość logiczną 1, „zakręcony” - wartość logiczną 0. Przepływ wody przez rurę realizuje koniunkcję stanów kurków. Opisany przykład został zilustrowany na poniższym rysunku.
W pneumatyce zawór pneumatyczny, posiadający dwa wejścia i jedno wyjście to zawór koniunkcji. Sygnał na wyjściu pojawia się tylko wtedy, gdy istnieją równocześnie dwa sygnały wejściowe. Zawór realizuje funkcję logiczną iloczynu logicznego (AND).
Pytania
Jakie można znaleźć zastosowanie dla iloczynu logicznego w praktyce?
Koniunkcja jest stosowana przez programistów w informatyce. W różnych językach programowania (C++, PHP, JavaScript) stosuje się iloczyn bitowy (operacja AND). Jest to operator dwuargumentowy. Operatorem dla koniunkcji jest najczęściej symbol &. Iloczyn bitowy jest operacją, w wyniku której włączane są tylko te bity, które są włączone w obu argumentach. Bardzo dobrze ilustruje to poniższa tabelka:
| a | b | a & b |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
A oto przykład operacji koniunkcji (AND) dla liczby zapisanej w systemie binarnym: 10001101 & 11001000 = 10001000. To samo w systemie dziesiętnym wygląda następująco: 141 & 200 = 136. Operacje takie możesz poćwiczyć za pomocą systemowego kalkulatora (Windows, wybierając kalkulator programisty).
Czy jest koniunkcja w Excelu?
Tak. To prosta i często wykorzystywana formuła, która w polskiej wersji językowej Excela nosi nazwę „=ORAZ”. Jako argumenty podajemy warunki logiczne. Jeżeli wszystkie zostaną spełnione, funkcja ta zwróci prawdę, w przeciwnym razie fałsz.
Przykład:
- Wpisz w komórkę B2 wartość 1.
- Wpisz w komórkę B3 wartość 1.
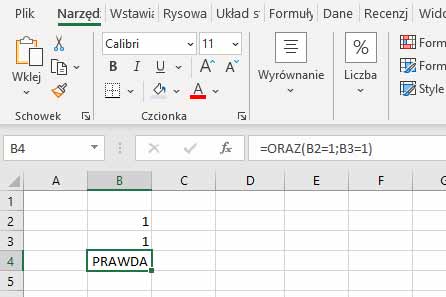
- Wpisz w komórkę B4 wyrażenie „=ORAZ(B2=1;B3=1)”.
- Gdy naciśniesz ENTER, otrzymasz wynik PRAWDA. Dzieje się tak dlatego, że sprawdzasz, czy w komórce B2 i B3 jest wartość 1. A taka wartość jest wpisana w obu komórkach.
- Zmień teraz wartość komórki B2 lub B3 na inną niż 1. Otrzymasz wówczas wartość FAŁSZ w komórce B4.
Co to jest zaprzeczenie koniunkcji?
Zaprzeczenie koniunkcji opisuje I prawo de Morgana.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Określ wartość logiczną zdań:
A. \((1<3) \wedge (2<6)\)
B. \((3<1) \wedge (2<6)\)
C. \((3<1) \wedge (6<2)\)
D. \((1<3) \wedge (6<2)\)
Inne zagadnienia z tej lekcji
© medianauka.pl, 2008-05-28, A-42
Data aktualizacji artykułu: 2023-02-06


 Zdanie logiczne
Zdanie logiczne Negacja
Negacja Alternatywa
Alternatywa Równoważność zdań
Równoważność zdań Prawa de Morgana
Prawa de Morgana