Układ nierówności
Analogicznie do układów równań możemy rozpatrywać układy nierówności. Na przykład:
\(\begin{cases}a_1x+b_1y>c_1 \\ a_2x+b_2y\leq{c_2}\end{cases}\)
Podano tutaj przykładowe znaki nierówności. Ze względu na możliwy kierunek i rodzaj nierówności otrzymujemy wiele możliwości różnych układów nierówności.
Jeżeli obie nierówności w układzie nierówności są nierównościami pierwszego stopnia, to układ taki nazywamy układem dwóch nierówności pierwszego stopnia z dwiema niewiadomymi.
Rozwiązanie układu nierówności
Zbiór wszystkich par liczb \((x,y)\), które spełniają jednocześnie obie nierówności, nazywamy rozwiązaniem układu tych nierówności.
Przykłady
Oto przykład układu nierówności:
\(\begin{cases}x+y>0\\x-y<1\end{cases}\)
Para liczb \((3,4)\) jest jednym z rozwiązań powyższego układu nierówności. Możemy to sprawdzić, podstawiając te liczby do obu nierówności.
\(\begin{cases}3+4>0\\3-4<1\end{cases}\)
\({\begin{cases}7>0\\-1<1\end{cases}}\)
Rozwiązać układ nierówności, to znaczy znaleźć wszystkie rozwiązania tego układu nierówności albo wykazać, że jest nim zbiór pusty. Zbiór rozwiązań układu nierówności jest iloczynem rozwiązań (częścią wspólną) wszystkich zbiorów rozwiązań poszczególnych nierówności układu.
Graficzne rozwiązywanie układu nierówności
Układy nierówności najłatwiej rozwiązać graficznie.
Wystarczy wykreślić wykresy obu nierówności i zakreskować część wspólną obu zbiorów rozwiązań, tak jak to zrobiono w poniższym przykładzie.
Przykłady
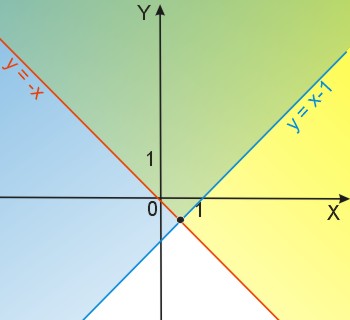
Rozwiąż graficznie układ nierówności i podaj interpretację geometryczną układu nierówności:
\(\begin{cases}x+y>0\\x-y<1\end{cases}\)
Wyznaczmy \(y\) z obu nierówności:
\(\begin{cases}y>-x\\-y<1-x/\cdot{(-1)}\end{cases}\)
\(\begin{cases}y>-x\\y>x-1\end{cases}\)
Wykreślamy w układzie współrzędnych proste o równaniach: \(y=-x\) oraz \(y=x-1\) i zaznaczamy obszary rozwiązań obu nierówności (na żółto \(y>-x\) i na niebiesko \(y>x-1\)).
Rozwiązanie układu tych nierówności reprezentuje obszar będący częścią wspólną wcześniej zaznaczonych obszarów (zielonkawy kolor) . Ponieważ nierówności są ostre, punkty należące do prostych nie należą do wykresu układu nierówności.
Zadania z rozwiązaniami

Zadanie nr 1.
Rozwiązać graficznie układ nierówności
\(\begin{cases}y<3x+1 \\ y<-3x+1 \\y>x-1 \end{cases}\)

Zadanie nr 2.
Dany jest układ nierówności
\(\begin{cases}x>-1 \\ x<1 \\y>-1\\ y<1 \end{cases}\)
Który z punktów: \(A(0,0), B(1,1), C(0,-1)\) należy do graficznego rozwiązania układu nierówności?

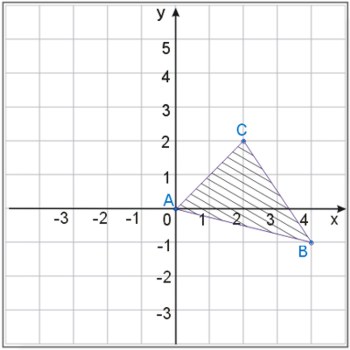
Zadanie nr 3.
Opisać za pomocą wzoru zbiór przedstawiony na rysunku, wiedząc, że punkty A, B i C mają całkowite współrzędne.

Zadanie nr 4.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x-y<1 \\ x+y\geq 1 \end{cases}\)

Zadanie nr 5.
Rozwiązać układ nierówności:
\(\begin{cases}2y+x<1\\-2y-x<-2 \end{cases}\)
© medianauka.pl, 2023-05-05, A-261
