Zadanie maturalne nr 8, matura 2014

Rozwiązanie zadania

Trapez jest to czworokąt, który ma co najmniej jedną parę boków równoległych. Dany jest punkt \(C\) i prosta na której leży podstawa \(AB\). Punkt \(C\) nie leży na tej prostej, bo należy do drugiej podstawy. Zatem prosta, która zawiera podstawę \(CD\) jest równoległa do prostej o równaniu \(y=2x-4\). Proste są równoległe, gdy ich współczynniki kierunkowe są równe (w przypadku danej prostej \(a=2\)). Mamy więc już pewną postać równania szukanej prostej:

\(y=2x+b\)

Aby znaleźć współczynnik \(b\), wystarczy podstawić za \(x\) i \(y\) współrzędne punktu \(C\), który leży na tej prostej:

\(C=(0,2)\)

\(y=2x+b\)

\(2=2\cdot 0+b\)

\(b=2\)

Zatem szukana prosta jest opisana równaniem \(y=2x+2\).

Odpowiedź

© medianauka.pl, 2017-01-31, ZAD-3431

Zadania podobne

Długość jednej z podstaw trapezu jest dwa razy większa od długości drugiej podstawy. Długość środkowej równoległej do podstaw jest równa 3. Obliczyć długości podstaw tego trapezu.

W trapezie prostokątnym długość podstaw jest równa odpowiednio 3 i 6, a długość krótszego z ramion 2. Oblicz długość dłuższego ramienia trapezu.

Wysokość trapezu równoramiennego o kącie ostrym 60° i ramieniu długości \(2\sqrt{3}\) jest równa:

A. \(\sqrt{3}\)

B. \(3\)

C. \(2\sqrt(3)\)

D. \(2\)

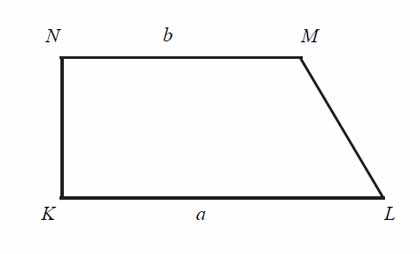
Dany jest trapez prostokątny \(KLMN\), którego podstawy mają długości \(KL=a, MN=b,
a>b\). Kąt \(KLM\) ma miarę 60°. Długość ramienia \(LM\) tego trapezu jest równa:

A. \(a-b\)

B. \(2(a-b)\)

C. \(a+\frac{b}{2}\)

D. \((a+b)/2\)

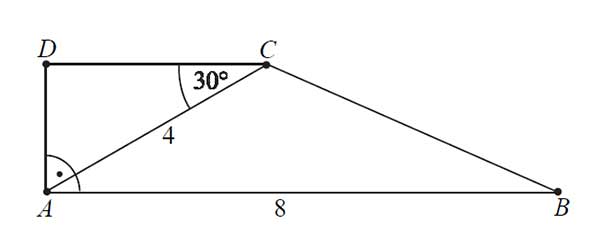
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość 8. Przekątna AC tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze (zobacz rysunek). Oblicz długość przekątnej \(BD\) tego trapezu.

Podstawą ostrosłupa czworokątnego ABCDS jest trapez \(ABCD (AB||CD)\). Ramiona tego trapezu mają długości \(AD=10\) i \(BC=16\), a miara kąta \(ABC\) jest równa 30°. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt α, taki, że \(tg\alpha =\frac{9}{2}\). Oblicz objętość tego ostrosłupa.