Zadanie maturalne nr 15, matura 2020 - poziom rozszerzony

Rozwiązanie zadania

Oznaczmy przez\(x\) dłuższą krawędź ekranu, a przez \(y\) krótszą krawędź. Posługujmy się milimetrami. Pole powierzchni ekranu jest więc równe:

\(60\ cm^2=60\ (10\ mm)^2=6000\ mm^2\)

Z warunków zadania wiemy, że:

\(xy=6000\)

\(y=\frac{6000}{x}\).

Pole powierzchni ekranu wraz z krawędziami wynosi:

\(P=(x+10)(x+6)=xy+6x+10y+60\)

\(P=6000+6x+10\cdot \frac{6000}{x}+60\)

\(P=6x+\frac{60000}{x}+6060\)

Mamy pole powierzchni urządzenia wyrażone poprzez zmienną x. Aby obliczyć ekstremum tej funkcji obliczamy pochodną funkcji \(P(x)\) względem \(x\).

\(P'(x)=6-\frac{60000}{x^2}=\frac{6x^2}{x^2}-\frac{60000}{x^2}=\frac{6(x^2-10000)}{x^2}\)

Jeżeli funkcja ma ekstremum w pewnym punkcie  i ma w tym punkcie pochodną, to pochodna w tym punkcie jest równa zeru.

\(P'(x)=0\)

\(\frac{6(x^2-10000)}{x^2}=0/:6\)

\(\frac{(x-100)(x+100)}{x^2}=0\)

Mamy dwa pierwiastki tego równania: 100 i -100.

Przyjrzyjmy się warunkom zadania. Określimy jeszcze dziedzinę rozwiązań:

Zakładamy, że jedna z krawędzi jest dłuższa od drugiej i obie mają dodatnią długość: \(x+10>y+6>0\). Zatem:

\(x+10>y+6\)

\(x+10-6>\frac{6000}{x}\)

\(x+4>\frac{6000}{x}/ \cdot x (x>0)\)

\(x^2+4x>6000\)

\(x^2+4x+4>6000+4\)

\((x+2)^2>6004\)

\(|x+2|>\sqrt{4\cdot 1501}\)

\(x+2>2\sqrt{1501}\)

\(x>2\sqrt{1501}-2\approx 76\)

Zatem pierwiastek \(-100\) nie należy do dziedziny rozwiązań. Pochodna \(P'(x)\) jest ujemna dla wartości poniżej 100 (i powyżej \(2\sqrt{1501}-2\approx 76\)), a większa dla wartości powyżej 100, zatem w tym miejscu ma minimum.

\(x_{min}=100\ mm\)

\(y_{min}=\frac{6000}{x_{min}}=60\ mm\)

Odpowiedź

© medianauka.pl, 2023-03-20, ZAD-4788

Zadania podobne

Rzucony kamień zakreśla w powietrzu tor opisany równaniem \(y=x-x^2\). Jakie jest maksymalne wzniesienia kamienia?

Jakie wymiary powinna mieć metalowa puszka w kształcie walca, aby przy określonej pojemności \(V\) zużyć możliwie najmniej blachy do jej wykonania?

Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(- 2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek).

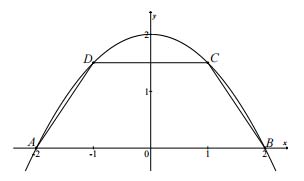
Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.

Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 144 m³. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów.

Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 1 m² dna
– 75 zł za 1 m² ściany bocznej.

Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.

a) Wykaż, że pole \(P\) każdego z tych trójkątów, jako funkcja długości \(b\) ramienia, wyraża się wzorem \(P(b)=\frac{(18-2b)\cdot \sqrt{18b-81}}{2}\).

b) Wyznacz dziedzinę funkcji \(P)\.

c) Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.