Zadanie - zastosowanie pochodnej funkcji w zadaniu z treścią
Treść zadania:
Jakie wymiary powinna mieć metalowa puszka w kształcie walca, aby przy określonej pojemności \(V\) zużyć możliwie najmniej blachy do jej wykonania?
 Rozwiązanie zadania
Rozwiązanie zadania
Rysunek przedstawia kształt puszki. Wprowadzamy oznaczenia:
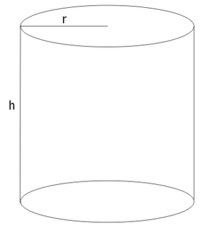
h - wysokość puszki (walca)
r - promień podstawy puszki (koła)
V - objętość walca (pojemność puszki)
S - pole powierzchni walca (ilość zużytej blachy)
Korzystamy ze wzoru na pole powierzchni walca:
Jeśli go nie pamiętasz, łatwo go można sobie wyprowadzić. Pole powierzchni walca jest równe polu obu podstaw (dwa razy pole koła) oraz polu powierzchni ściany bocznej (prostokąt o bokach długość równych wysokości walca oraz obwodowi koła, stanowiącego podstawę walca).
Mamy funkcję dwóch zmiennych (r i h). Skorzystajmy więc z danego w zadaniu V, czyli wzoru na objętość walca (pole podstawy razy wysokość):
Z drugiego równania wyznaczymy \(h\) w wstawimy do wzoru na pole powierzchni.
\(V=\pi r^2h/:\pi r^2 \)
\(h=\frac{V}{\pi r^2}\)
\(S=2\pi r^2+2\pi rh\)
\(S=2\pi r^2+2\cancel{\pi r} \cdot \frac{V}{\cancel{\pi} r^{\cancel{2}}}\)
\(S=2\pi r^2+\frac{2V}{r}\)
Mamy do czynienia z funkcją jednej zmiennej \(r\) (V jest daną liczbą). Szukamy minimum (ekstremum) w punktach w których pochodna przyjmuje wartość zero. Obliczamy więc pochodną funkcji \(S(r)\) (względem zmiennej \(r\))
\(S=2\pi r^2+2V\cdot r^{-1} \)
\(S'=2\pi \cdot 2r+2V\cdot (-1)\cdot r^{-2}\)
\(S'=4\pi r-\frac{2V}{r^2}\)
Pochodna jest równa zeru:
\(S'=0\)
\(4\pi r-\frac{2V}{r^2}=0\)
\(4\pi r\cdot \frac{r^2}{r^2}-\frac{2V}{r^2}=0\)
\(\frac{4\pi r^3-2V}{r^2}=0\)
Ułamek jest równy zeru, gdy jego licznik jest równy zero.
\(4\pi r^3-2V=0\)
\(4\pi r^3=2V/:4\pi\)
\(r^3=\frac{2V}{4\pi}\)
\(r=\sqrt[3]{\frac{2V}{4\pi}}\)
W tym punkcie mamy ekstremum o ile pochodna zmienia znak. Zbadajmy znak pochodnej:
\(S'>0\\ \frac{4\pi r^3-2V}{r^2}>0\)
W mianowniku ułamka jest kwadrat liczby (jest dodatni), więc licznik również musi być dodatni:
\(4\pi r^3-2V>0/:4\pi\)
\(r^3-\frac{2V}{4\pi}>0 \)
\(r^3-(\sqrt[3]{\frac{2V}{4\pi}})^3>0\)
Skorzystamy ze wzoru skróconego mnożenia:
Mamy więc:
\((r-\sqrt[3]{\frac{2V}{4\pi}})(r^2+2r\sqrt[3]{\frac{2V}{4\pi}}+(\sqrt[3]{\frac{2V}{4\pi}})^2)>0\)
Drugi człon jest dodatni (mamy sumę dodatnich czynników), a iloczyn dwóch liczb jest dodatni, gdy obie liczby są dodatnie lub ujemne (ten przypadek tutaj nie występuje). Możemy więc napisać, że:
\(r-\sqrt[3]{\frac{2V}{4\pi}}>0\)
\(r>\sqrt[3]{\frac{2V}{4\pi}}\)
Analogicznie możemy napisać, że:
\(S'<0 \Leftrightarrow r<\sqrt[3]{\frac{2V}{4\pi}}\)
Zatem w punkcie \(r=\sqrt[3]{\frac{2V}{4\pi}}\) pochodna przechodzi ze znaku ujemnego w dodatni - funkcja S(r) osiąga minimum
\(r_{min}=\sqrt[3]{\frac{2V}{4\pi}}\)
Musimy jeszcze znaleźć wymiar h:
\(h_{min}=\frac{V}{\pi r^2}=\frac{V}{\pi (\sqrt[3]{\frac{V}{2\pi}})^2}=\frac{V}{\pi \sqrt[3]{\frac{V^2}{4\pi ^2}}}=\frac{V\cdot \sqrt[3]{\frac{V}{2\pi}}}{\pi \sqrt[3]{\frac{V^2}{4\pi ^2}}\cdot \sqrt[3]{\frac{V}{2\pi}}}=\frac{V\sqrt[3]{\frac{V}{2\pi }}}{\pi\cdot \frac{V}{2\pi}}=\frac{1}{2}\sqrt[3]{\frac{V}{2\pi}}=2r_{min}\)
Zatem na wykonanie puszki zużyjemy najmniej blachy, jeżeli średnica (2 razy promień) podstawy będzie równa wysokości puszki.
 Odpowiedź
Odpowiedź
© medianauka.pl, 2010-09-29, ZAD-946


Zadania podobne
Zadanie nr 1.
Rzucony kamień zakreśla w powietrzu tor opisany równaniem \(y=x-x^2\). Jakie jest maksymalne wzniesienia kamienia?

Zadanie nr 2 — maturalne.
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(- 2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek).
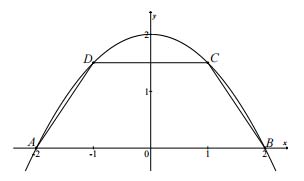
Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.

Zadanie nr 3 — maturalne.
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Zadanie nr 4 — maturalne.
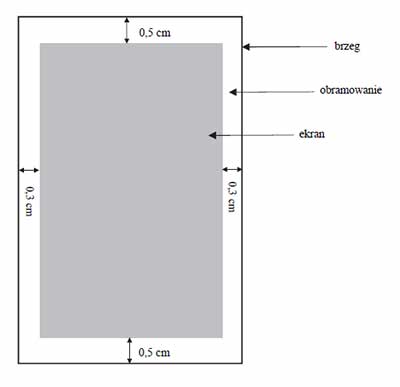
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 60 cm2. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.

Zadanie nr 5 — maturalne.
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 144 m3. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów.
Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 1 m2 dna
– 75 zł za 1 m2 ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

Zadanie nr 6 — maturalne.
Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.
a) Wykaż, że pole \(P\) każdego z tych trójkątów, jako funkcja długości \(b\) ramienia, wyraża się wzorem \(P(b)=\frac{(18-2b)\cdot \sqrt{18b-81}}{2}\).
b) Wyznacz dziedzinę funkcji \(P)\.
c) Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.

