Nauka » Matematyka » Pochodna w zadaniach z treścią

Zadanie - zadanie z treścią - zastosowanie pochodnej

Rzucony kamień zakreśla w powietrzu tor opisany równaniem

. Jakie jest maksymalne wzniesienia kamienia?

Rozwiązanie zadania uproszczone

$y'=1-2x\\ y'=0\Leftrightarrow 1-2x=0\\ 2x=1/:2 \\ x=\frac{1}{2}\\ y_{max}=\frac{1}{2}-(\frac{1}{2})^2=\frac{1}{4}$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Mamy już ułatwione zadanie, gdyż podane jest gotowe równanie jednej zmiennej. Szukamy maksymalnego wzniesienia kamienia, czyli maksymalną wartość zmiennej y. Szukamy więc ekstremum funkcji y=f(x). W tym celu obliczamy pochodną:

Szukamy ekstremum funkcji w punkcie, w którym pochodna jest równa zeru:

$y'=0\\ 1-2x=0 \\ 2x=1/:2 \\ x=\frac{1}{2}$

W tym punkcie funkcja osiąga ekstremum, o ile zmienia w tym punkcie znak z ujemnego na dodatni lub z dodatniego na ujemny. Jak widać dla wartości mniejszych od 1/2 pochodna funkcji y'=1-2x przyjmuje dodatnie wartości, a dla x większych od 1/2 pochodna jest ujemna. Zatem funkcja osiąga w tym miejscu maksimum. Obliczmy wartość funkcji w tym punkcie:

$f(\frac{1}{2})=\frac{1}{2}-(\frac{1}{2})^2=\frac{1}{2}-\frac{1}{4}=\frac{2}{4}-\frac{1}{4}=\frac{1}{4}$

Odpowiedź

Maksymalne wzniesienie kamienia wynosi 1/4

Zadania podobne

Zadanie - zastosowanie pochodnej funkcji w zadaniu z treścią
Jakie wymiary powinna mieć metalowa puszka w kształcie walca, aby przy określonej pojemności V zużyć możliwie najmniej blachy do jej wykonania?

Pokaż rozwiązanie zadania

Zadanie maturalne nr 16, matura 2016 (poziom rozszerzony)
Parabola o równaniu $y=2-\frac{1}{2}x^2$ przecina oś Ox układu współrzędnych w punktach A = (- 2,0) i B = (2,0). Rozpatrujemy wszystkie trapezy równoramienne ABCD, których dłuższą podstawą jest odcinek AB, a końce C i D krótszej podstawy leżą na paraboli (zobacz rysunek).
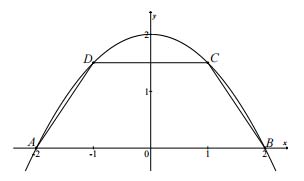
Zadanie 16, ilustracja, matura 2016

Wyznacz pole trapezu ABCD w zależności od pierwszej współrzędnej wierzchołka C. Oblicz współrzędne wierzchołka C tego z rozpatrywanych trapezów, którego pole jest największe.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 16, matura 2015 (poziom rozszerzony)
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 15, matura 2020 - poziom rozszerzony

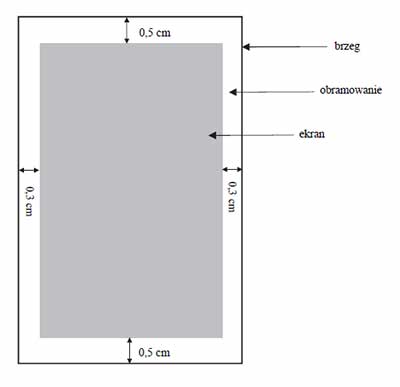
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 60 cm². Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.

zadanie maturalne 15, matura rozszerzona 2020

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.