Monotoniczność ciągu
Ciąg rosnący jest to taki ciąg \((a_n)\), w którym każdy następny wyraz jest większy od poprzedniego, czyli \(a_{n+1}-a_n>0\) dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu k-elementowego.
Ciąg malejący jest to taki ciąg \((a_n)\), w którym każdy następny wyraz jest mniejszy od poprzedniego, czyli \(a_{n+1}-a_n<0\) dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu k-elementowego.
Ciąg niemalejący jest to taki ciąg \((a_n)\), w którym każdy następny wyraz jest większy od poprzedniego, czyli \(a_{n+1}-a_n\geq0\) dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu k-elementowego.
Ciąg nierosnący jest to taki ciąg \((a_n)\), w którym każdy następny wyraz jest mniejszy od poprzedniego, czyli \(a_{n+1}-a_n\leq 0\) dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu k-elementowego.
Ciąg stały jest to taki ciąg \((a_n)\), w którym każdy wyraz jest stały, czyli \(a_{n+1}-a_n=0\) dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu k-elementowego.
Jak zbadać monotoniczność ciągu?
Badanie monotoniczności ciągu sprowadza się do zbadania znaku różnicy \(a_{n+1}-a_n\). Przeanalizujmy to na przykładzie.
Przykład 1
Zbadać monotoniczność ciągu \(a_n=2n\).
Mamy:
\(a_n=2n\)
\(a_{n+1}=2(n+1)=2n+2\)
Badamy różnicę:
\(a_{n+1}-a_n=2n+2-2n=2>0\)
Różnica następnego i poprzedniego wyrazu jest dodatnia, więc ciąg jest rosnący.
Przykład 2
Zbadaj monotoniczność ciągu \(a_n=\frac{n+1}{n}\).
Mamy:
\(a_n=\frac{n+1}{n}\)
\(a_{n+1}=\frac{(n+1)+1}{n+1}=\frac{n+2}{n+1}\).
Badamy różnicę
\(a_{n+1}-a_n=\frac{n+2}{n+1}-\frac{n+1}{n}=\frac{n(n+2)}{n(n+1)}-\frac{(n+1)^2}{n(n+1)}=\)
\(=\frac{n^2+2n-n^2-2n-1}{n(n+1)}=\frac{-1}{n(n_1)}<0\)
Różnica następnego i poprzedniego wyrazu jest ujemna. Wyrażenie \(n(n+1)\) jest większe od zera, ponieważ \(n\) jest liczbą naturalną, więc ciąg jest malejący.
Ciągi niemonotoniczne
Nie każdy ciąg liczbowy jest monotoniczny. Oto przykłady ciągów niemonotonicznych, czyli takich, które nie są ciągami niemalejącymi ani nierosnącymi.
Przykłady
- \((1,-1,2,-2,3,-3, ...)\)
- \((2,3,3,2,3,4,4,3, ...)\)
Zadania z rozwiązaniami

Zadanie nr 1.
Zbadać monotoniczność ciągu:
a) \(a_n=n^2-2\)
b) \(a_n=\frac{(-1)^n}{n}\)
Powiązane materiały
© medianauka.pl, 2009-08-21, A-295
Data aktualizacji artykułu: 2023-05-10

 Ciąg liczbowy
Ciąg liczbowy Wykres ciągu
Wykres ciągu Pojęcie ciągu
Pojęcie ciągu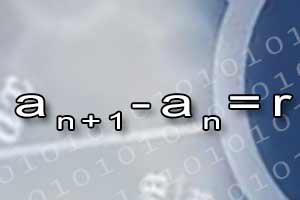 Ciąg arytmetyczny
Ciąg arytmetyczny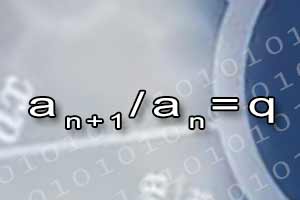 Ciąg geometryczny
Ciąg geometryczny