Wykres ciągu
Zauważmy, że bez problemu można sporządzić wykres dowolnego ciągu. Ponieważ argumentami są liczby naturalne, wartościami określone przez dany ciąg liczby, wykresem w układzie, gdzie osią odciętych będzie \(n\), a osią rzędnych, będzie \(a_n\) dyskretny zbiór punktów (zbiór punktów izolowanych).
Przykład
Naszkicuj wykres ciągu o wyrazach \(a_n=2n-5\).
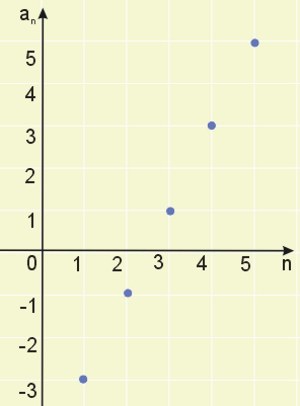
Wypiszmy najpierw kolejne wyrazy ciągu: \((-3, -1, 1, 3, 5, ... )\).
Mając już wypisane kolejne wyrazu ciągu, zaznaczamy w układzie współrzędnych pary liczb: kolejna liczba naturalna i kolejna wartość wyrazu ciągu: \((1,-3), (2,-1), (3, 1), (4, 3), (5, 5), ..., (n, 2n-5), ...\) W ten sposób powstaje nasz wykres. Sporządźmy ten wykres ciągu.
 Kalkulator
KalkulatorRysowanie wykresu ciągu
Wpisz dane:
an =
Wpisz wzór ciągu w okno edycyjne i wciśnij klawisz Rysuj, aby narysować wykres ciągu. Jeżeli klikniesz punkt na wykresie, wyświetlisz jego współrzędne w układzie.
Oprogramowanie: Natalia Okoń
Zadania z rozwiązaniami

Zadanie nr 2.
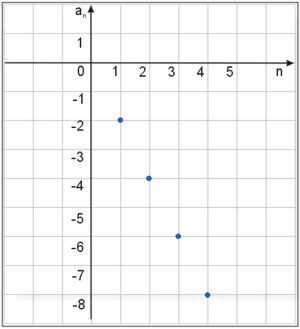
Znaleźć wzór na n-ty wyraz ciągu, którego fragment wykresu został przedstawiony na ilustracji:
Powiązane materiały
© medianauka.pl, 2009-08-20, A-294
Data aktualizacji artykułu: 2020-07-10

 Ciąg liczbowy
Ciąg liczbowy Monotoniczność ciągu
Monotoniczność ciągu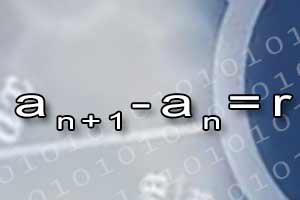 Ciąg arytmetyczny
Ciąg arytmetyczny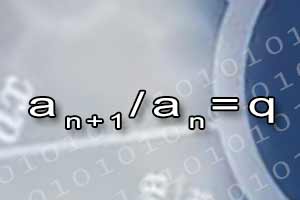 Ciąg geometryczny
Ciąg geometryczny Pojęcie ciągu
Pojęcie ciągu



