Pierścień kołowy

Definicja

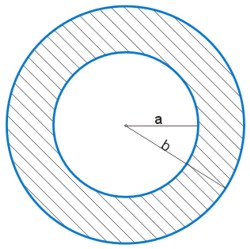
Pierścień kołowy jest to zbiór punktów płaszczyzny, których odległość od punktu \(A\) jest nie mniejsza niż \(a\) i nie większa niż \(b\), przy czym \(0<a<b\).

Liczbę \(a\) nazywamy promieniem małym pierścienia kołowego, natomiast liczbę \(b\) nazywamy promieniem dużym pierścienia kołowego.

Pierścień kołowy został zilustrowany na rysunku.

Pole pierścienia kołowego

Pole pierścienia kołowego o promieniu małym \(a\) i dużym \(b\) jest równe:

\(P=\pi (b^2-a^2)\)

Przykłady

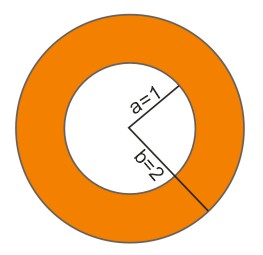
Obliczyć pole pierścienia kołowego przedstawionego na rysunku o promieniu 2 i 1.

Pole pierścienia kołowego obliczamy następująco:

\(P=\pi (b^2-a^2)=\pi \cdot (2^2-1^2)=\pi \cdot (4-1)=3\pi\)

Zadania z rozwiązaniami

Zadanie nr 1.

Obliczyć pole powierzchni pierścienia kołowego wyznaczonego przez okręgi \(x^2+y^2=4\) oraz \(x^2+y^2=16\).

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Pola dwóch kół współśrodkowych są równe odpowiednio 6 i 4. Oblicz pole pierścienia kołowego wyznaczonego przez te koła.

Pokaż rozwiązanie zadania.

Powiązane materiały

Łuk okręgu

Pole wycinka kołowego

Figury związane z okręgiem.

Okrąg i koło