
Zadanie maturalne nr 33, matura 2016 (poziom podstawowy)
Treść zadania:
Podstawą ostrosłupa prawidłowego trójkątnego \(ABCS\) jest trójkąt równoboczny \(ABC\). Wysokość \(SO\) tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa \(ABCS\) oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
Rozwiązanie zadania
Zaczynamy od szkicu i odpowiednich oznaczeń:
Aby wykorzystać daną objętość ostrosłupa, musimy znać pole podstawy, a bez znajomości długości krawędzi podstawy (boku trójkąta równobocznego) nic nie policzymy. Zaczynamy więc od wyznaczenia wielkości a na podstawie twierdzenia Pitagorasa.
\((|AB|)^2=(|BP|)^2+(|AP|)^2\)
\(a^2=(\frac{1}{2}a)^2+H^2\)
\(H^2=\frac{3}{4}a^2\)
\(H=\frac{\sqrt{3}a}{2}\)
Policzmy teraz pole podstawy, czyli pole trójkąta równobocznego.
\(P_p=\frac{1}{2}aH=\frac{1}{2}a\cdot \frac{\sqrt{3}a}{2}=\frac{\sqrt{3}a^2}{4}\)
Znamy objętość ostrosłupa. Skorzystamy z tego, wyznaczając wielkość \(a\). Przypomnę, że objętość ostrosłupa obliczamy mnożąc jedną trzecią pola podstawy przez wysokość tego ostrosłupa.
\(V=27=\frac{1}{3}P_p\cdot H\)
\(27=\frac{1}{3}\cdot \frac{\sqrt{3}a^2}{4}\cdot \frac{\sqrt{3}}{2}\)
\(27=\frac{a^3}{8}\)
\(a=6\)
\(H=\frac{\sqrt{3}\cdot 6}{2}=3\sqrt{3}\)
Aby policzyć pole powierzchni bocznej, musimy znać wielkość \(h\). Obliczymy ją z twierdzenia Pitagorasa. Zwracam tylko uwagę na to, że odcinek \(OP\) jest równy \(\frac{1}{3}\) długości \(H\), gdyż jest to trójkąt równoboczny, a punkt \(O\) jest środkiem okręgu opisanego na tym trójkącie.
\(|OP|=\frac{1}{3}H=\sqrt{3}\)
\(H=3\sqrt{3}\)
\(H^2+(|OP|)^2=h^2\)
\((3\sqrt{3})^2+(\sqrt{3})^2=h^2\)
\(h^2=30\)
\(h=\sqrt{30}\)
Pole powierzchni bocznej obliczamy jako trzy razy pole trójkąta \(BCS\):
\(P_{pb}=3\cdot \frac{1}{2}ah=3\cdot\frac{1}{2} \cdot 6\cdot \sqrt{30}=9\sqrt{30}\)
Ostatnia cześć zadania, to obliczenie cosinusa kata alfa.
\(\cos{\alpha}=\frac{|OP|}{h}=\frac{\sqrt{3}}{\sqrt{30}}=\frac{\sqrt{3}\cdot \sqrt{30}}{30}=\frac{\sqrt{10}}{10}\)
Odpowiedź
\(P_{pb}=9\sqrt{30}\)
\(\cos{\alpha}= \frac{\sqrt{10}}{10}\)
© medianauka.pl, 2016-11-01, ZAD-3259


Zadania podobne

Zadanie nr 1 — maturalne.
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 120°. Oblicz objętość tego ostrosłupa.

Zadanie nr 2 — maturalne.
Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Krawędź boczna \(SD\) jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi \(ABS\) i \(CBS\) tego ostrosłupa.

Zadanie nr 3 — maturalne.
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa:
A. 5
B. 7
C. 8
D. 10

Zadanie nr 4 — maturalne.
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest:
A. sześć razy dłuższa od wysokości walca.
B. trzy razy dłuższa od wysokości walca.
C. dwa razy dłuższa od wysokości walca.
D. równa wysokości walca.

Zadanie nr 5 — maturalne.
Podstawą ostrosłupa jest kwadrat \(KLMN\) o boku długości \(4\). Wysokością tego ostrosłupa jest krawędź \(NS\), a jej długość też jest równa \(4\) (zobacz rysunek).
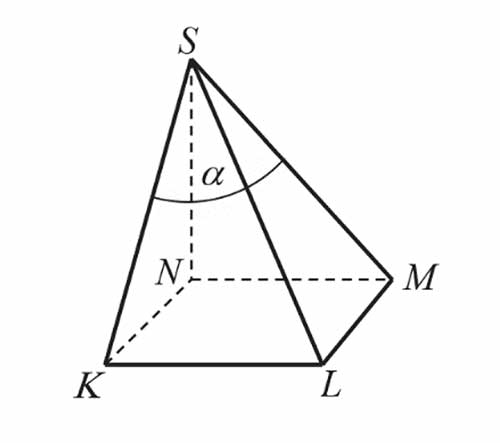
Kąt \(\alpha\), jaki tworzą krawędzie \(KS\) i \(MS\), spełnia warunek
- \(\alpha=45°\)
- \(45°<\alpha <60°\)
- \(\alpha >60°\)
- \(\alpha =60°\)

Zadanie nr 6 — maturalne.
Przekrój ostrosłupa prawidłowego trójkątnego \(ABCS\) płaszczyzną przechodzącą przez wierzchołek S i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość \(\frac{4\sqrt{3}}{3}\). Oblicz objętość tego ostrosłupa.

Zadanie nr 7 — maturalne.
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
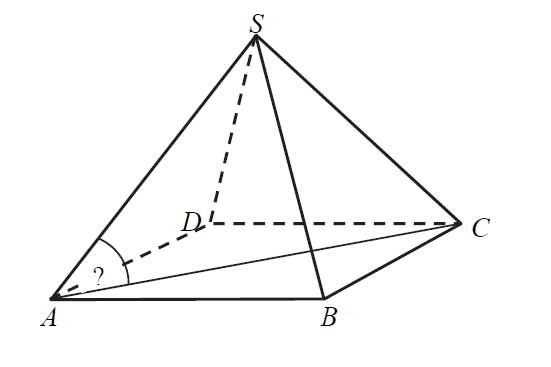
Miara kąta SAC jest równa
A. 90°
B. 75°
C. 60°
D. 45°

Zadanie nr 8 — maturalne.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt \(\alpha\) jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta \(\alpha\).
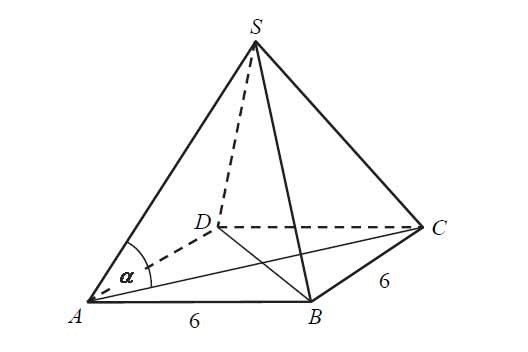

Zadanie nr 9 — maturalne.
Podstawą ostrosłupa \(ABCDS\) jest prostokąt \(ABCD\), którego boki mają długości \(|AB|=32\) i \(|BC|=18\). Ściany boczne \(ABS\) i \(CDS\) są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem \(\alpha\). Ściany boczne \(BCS\) i \(ADS\) są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem \(\beta\) . Miary kątów \(\alpha\) i \(\beta\) spełniają warunek: \(\alpha+\beta=90°\). Oblicz pole powierzchni całkowitej tego ostrosłupa.

Zadanie nr 10 — maturalne.
Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\), którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy, pod kątem którego tangens jest równy \(\sqrt{7}\). Oblicz objętość tego ostrosłupa.


Zadanie nr 11 — maturalne.
Podstawą ostrosłupa czworokątnego ABCDS jest trapez \(ABCD (AB||CD)\). Ramiona tego trapezu mają długości \(AD=10\) i \(BC=16\), a miara kąta \(ABC\) jest równa 30°. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt α, taki, że \(tg\alpha =\frac{9}{2}\). Oblicz objętość tego ostrosłupa.

Zadanie nr 12 — maturalne.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30° i ma długość równą 6 (zobacz rysunek).
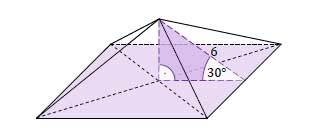
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.

Zadanie nr 13 — maturalne.
W pewnym ostrosłupie prawidłowym stosunek liczby \(W\) wszystkich wierzchołków do liczby \(K\) wszystkich krawędzi jest równy \(\frac{W}{K}=\frac{3}{5}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Podstawą tego ostrosłupa jest
A. kwadrat.
B. pięciokąt foremny.
C. sześciokąt foremny.
D. siedmiokąt foremny.

