Zadanie - kąt zewnętrzny
Treść zadania:
Ile wynosi miara kąta zewnętrznego w ośmiokącie foremnym?
Rozwiązanie zadania
Wzór na miarę kąta wewnętrznego w wielokącie foremnym jest następujący:
\(\alpha=180^o-\frac{360^o}{n}\)Wyprowadzenie tego wzoru znajdziesz tutaj.
Na rysunku kąt zewnętrzny został oznaczony grecką literą \(\delta\). Kąty o tych samych miarach oznaczono tymi samymi kolorami oraz literami. Ich miary są równe ze względu na to, że kąty te są kątami wierzchołkowymi.
Suma miar wszystkich zaznaczonych kątów jest równa mierze kata pełnego:
\(2\alpha+2\delta=360^o/:2 \)
\(\alpha+\delta=180^o\)
\(\delta=180^o-\alpha\)
Korzystając ze wzoru wyżej zacytowanego na miarę kąta wewnętrznego wielokąta foremnego, przy \(n=8\) mamy:
\(\delta=180^o-(180^o-\frac{360^o}{n})\)
\(\delta=\frac{360^o}{n}\)
\(\delta=\frac{360^o}{8}=45^o\)
Odpowiedź
\(\delta=45^o\)© medianauka.pl, 2011-01-13, ZAD-1098


Zadania podobne
Zadanie nr 1.
Obliczyć miarę kąta wewnętrznego (pomiędzy sąsiednimi bokami) n-kąta foremnego.
Zadanie nr 2.
Miara kąta wewnętrznego (pomiędzy sąsiednimi bokami) pewnego wielokąta foremnego jest równa 162°. Ile boków ma ten wielokąt?

Zadanie nr 3 — maturalne.
Punkty \(A, B, C\) i \(D\) leżą na okręgu o środku S. Miary kątów \(SBC, BCD, CDA\) są równe odpowiednio: \(|\angle SBC|=60°, |\angle BCD|=110°, |\angle CDA|=90°\) (zobacz rysunek).
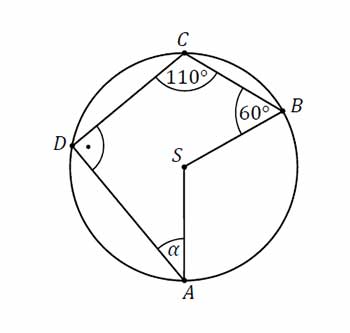
Wynika stąd, że miara \(\alpha\); kąta \(DAS\) jest równa
A. 25°
B. 30°
C. 35°
D. 40°

Zadanie nr 4 — maturalne.
Czworokąt \(ABCD\), w którym \(|BC|=4\) i \(|CD=5|\), jest opisany na okręgu. Przekątna \(AC\) tego czworokąta tworzy z bokiem \(BC\) kąt o mierze 60°, natomiast z bokiem \(AB\) – kąt ostry, którego sinus jest równy \(\frac{1}{4}\) . Oblicz obwód czworokąta \(ABCD\). Zapisz obliczenia.






