Zadanie - geometria analityczna
Treść zadania:
Na średnicy okręgu o promieniu długości 6 obrano punkt \(A\) w taki sposób, że punkt ten dzieli promień okręgu w stosunku 1 do 2 (krótszy odcinek znajduje się bliżej okręgu). Obliczyć obwód trójkątów wyznaczonych przez średnicę i odcinek prostopadłej przechodzący przez punkt \(A\).
Rozwiązanie zadania
Sporządzamy rysunek.
Mamy dwa trójkąty prostokątne, których obwody należy obliczyć. Podział promienia w stosunku 1/2 oznacza, że jeżeli promień ma długość \(6\), to punkt \(A\) dzieli go na dwie części, jedna o długości \(2\), druga o długości \(6-2=4\). Mamy następujące dane.
\(|ON|=r=6\)
\(|OA|=4\)
\(|AN|=2\)
\(|AM|=10\)
\(h=?\)
\(x=?\)
\(y=?\)
Gdy poznamy długość odcinka \(h\), korzystając z twierdzenia Pitagorasa, wyznaczymy pozostałe niewiadome. Aby wyznaczyć \(h\), korzystamy z twierdzenia, które mówi że odcinek prostopadłej opuszczonej z dowolnego punktu okręgu na średnicę jest średnią geometryczną odcinków, na które ta prostopadła dzieli średnicę.
\(h=\sqrt{x_sy_s}\)Mamy więc:
\(h=\sqrt{|AM|\cdot |AN|}=\sqrt{2\cdot 10}=\sqrt{20}=2\sqrt{5}\)
Do wyznaczenia x oraz y skorzystamy z twierdzenia Pitagorasa. Wyznaczamy \(y\):
\(y^2=|AM|^2+h^2\)
\(y^2=10^2+(2\sqrt{5})^2\)
\(y^2=100+20\)
\(y^2=120\)
\(y=\sqrt{120}\)
\(y=2\sqrt{30}\)
Wyznaczamy \(x\):
\(x^2=|AN|^2+h^2\)
\(x^2=2^2+(2\sqrt{5})^2\)
\(x^2=4+20\)
\(x^2=24\)
\(x=\sqrt{24}\)
\(x=2\sqrt{6}\)
Możemy teraz wyznaczyć obwody obu trójkątów:
\(L_{MAB}=|MA|+y+h=10+2\sqrt{30}+2\sqrt{5}\)
\(L_{NAB}=|NA|+y+h=2+2\sqrt{6}+2\sqrt{5}\)
Odpowiedź
\(L_{MAB}=10+2\sqrt{30}+2\sqrt{5}\)
\(L_{NAB}=2+2\sqrt{6}+2\sqrt{5}\)
© medianauka.pl, 2011-01-15, ZAD-1101


Zadania podobne
Zadanie nr 1.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).

Zadanie nr 3 — maturalne.
Punkty \(ABCD\) leżą na okręgu o środku \(S\) (zobacz rysunek). Miara kąta \(BDC\) jest równa:
A. 91°
B. 72,5°
C. 18°
D. 32°

Zadanie nr 4 — maturalne.
Miara kąta wpisanego w okrąg jest o \(20°\) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa:
A. \(5°\)
B. \(10°\)
C. \(20°\)
D. \(30°\)

Zadanie nr 5 — maturalne.
Środek \(S\) okręgu opisanego na trójkącie równoramiennym \(ABC\), o ramionach \(AC\) i \(BC\), leży wewnątrz tego trójkąta (zobacz rysunek).
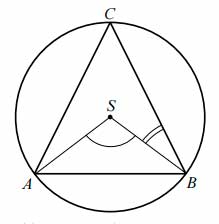
Wykaż, że miara kąta wypukłego \(ASB\) jest cztery razy większa od miary kąta wypukłego \(SBC\).

Zadanie nr 6 — maturalne.
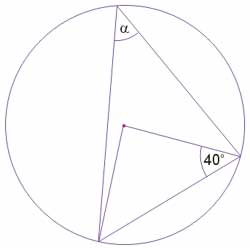
Na okręgu o środku w punkcie \(O\) leży punkt \(C\) (zobacz rysunek). Odcinek \(AB\) jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy \(\alpha\) ma miarę:
A. \(m=116°
B. \(m=114°
C. \(m=112°
D. \(m=110°

Zadanie nr 7 — maturalne.
Dany jest okrąg o środku \(S\). Punkty \(K, L\) i \(M\) leżą na tym okręgu. Na łuku \(KL\) tego okręgu są oparte kąty \(KSL\) i \(KML\) (zobacz rysunek), których miary \(\alpha\) i \(\beta\), spełniają warunek \(\alpha +\beta=111°\). Wynika stąd, że
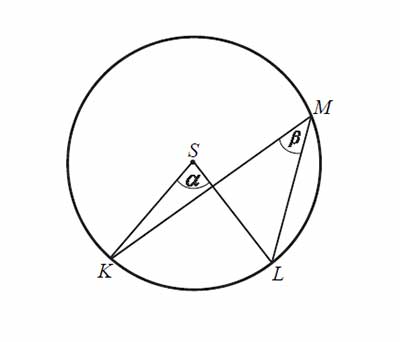
A. \(\alpha=74°\)
B. \(\alpha=76°\)
C. \(\alpha=70°\)
D. \(\alpha=72°\)

Zadanie nr 8 — maturalne.
Okręgi o środkach odpowiednio \(A\) i \(B\) są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku \(A\) jest równy 2.
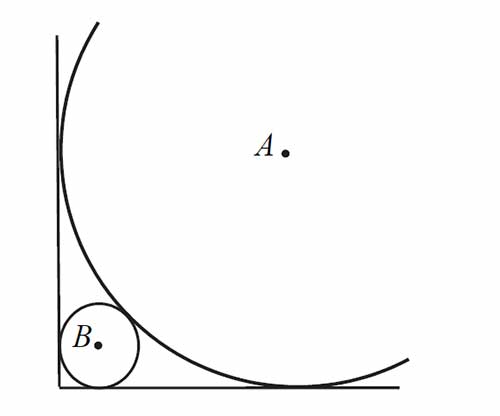
Uzasadnij, że promień okręgu o środku \(B\) jest mniejszy od \(\sqrt{2}-1\).

Zadanie nr 9 — maturalne.
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).
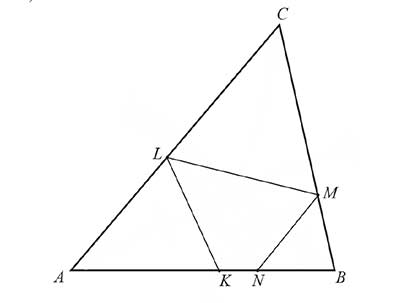
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.

Zadanie nr 10 — maturalne.
Punkty \(D\) i \(E\) leżą na okręgu opisanym na trójkącie równobocznym \(ABC\) (zobacz rysunek). Odcinek \(CD\) jest średnicą tego okręgu. Kąt wpisany \(DEB\) ma miarę \(\alpha\).
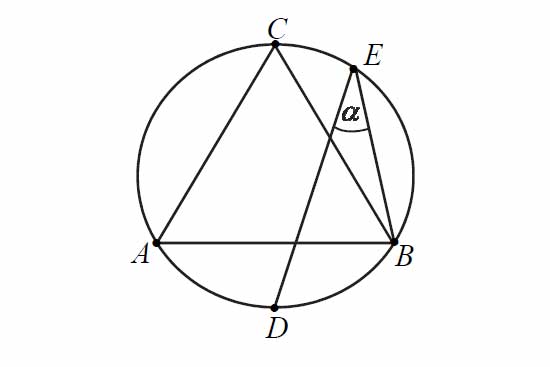
A. \(\alpha=30°\)
B. \(\alpha<30°\)
C. \(\alpha>45°\)
D. \(\alpha=45°\)

Zadanie nr 11 — maturalne.
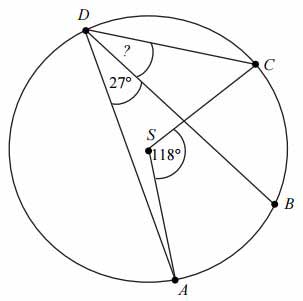
Punkty \(A, B, C, D\) leżą na okręgu o środku w punkcie \(O\). Kąt środkowy \(DOC\) ma miarę 118° (zobacz rysunek).

Miara kąta ABC jest równa
A. 59°
B. 48°
C. 62°
D. 31°

Zadanie nr 12 — maturalne.
Punkty A, B, C leżą na okręgu o środku S. Punkt D jest punktem przecięcia cięciwy AC i średnicy okręgu poprowadzonej z punktu B. Miara kąta BSC jest równa α, a miara kąta ADB jest równa γ (zobacz rysunek).
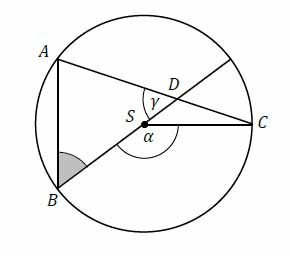
Wtedy kąt ABD ma miarę
A. \(\frac{\alpha}{2}+\gamma−180°\)
B. \(180°-\frac{\alpha}{2}-\gamma\)
C. \(180°-\alpha-\gamma\)
D. \(\alpha+\gamma−180°\)

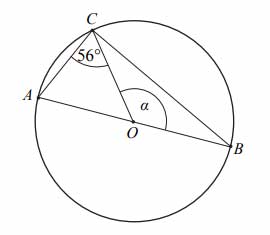
Zadanie nr 13 — maturalne.
Punkty \(A, B, C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę 70° (zobacz rysunek). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta ostrego \(ABC\) jest równa:
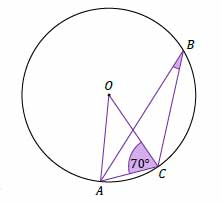
A. \(10°\)
B. \(20°\)
C. \(35°\)
D. \(40°\)