Zadanie - trójkąt w układzie współrzędnych
Treść zadania:
Dany jest trójkąt o wierzchołkach \(A=(-1,0), B=(1,-1)\) i \(C=(1,2)\). Oblicz długość wysokości tego trójkąta opuszczonej z wierzchołka C.
Rozwiązanie zadania
Sporządzamy szkic:
Szukamy długości wysokości \(h\). Wysokość leży na prostej \(b\), która jest prostopadła do prostej a zawierającej podstawę \(AB\) trójkąta. Znając współrzędne punktu \(D\), który jest punktem wspólnym obu prostych (wystarczy rozwiązać układ równań) obliczymy odległość między punktami \(C, D\), która jest równa długości wysokości.
Szukamy równania prostej \(a\). Korzystamy z równania prostej:
\(y=ax+b\)
Dane są współrzędne punktów \(A\) i \(B\), więc:
\(A=(-1,0), \ B=(1,-1)\)
\(y=ax+b\)
\(\begin{cases}-1=a\cdot 1+b\\(0=a\cdot (-1)+b \end{cases} \)
\(\begin{cases}-1=a+b\\(0=-a+b \end{cases} \)
\(\begin{cases}-1=b+b/:2\\(a=b \end{cases} \)
\(\begin{cases} b=-\frac{1}{2}\\(a=-\frac{1}{2} \end{cases}\)
\(y=-\frac{1}{2}x-\frac{1}{2}\)
Szukamy teraz równania prostej \(b\), która zawiera wysokość. Ponieważ proste \(a\) i \(b\) są prostopadłe do siebie, ich współczynniki kierunkowe są w stosunku do siebie przeciwne i odwrotne:
Korzystając z tego, jak również z danych współrzędnych punktu \(C\), otrzymujemy:
\(y=a_1x+b_1\)
\(a_1=-\frac{1}{a}=-\frac{1}{-\frac{1}{2}}=2\)
\(y=2x+b_1\)
\(C=(1,2)\)
\(2=2\cdot 1+b_1\)
\(2=2+b_1\)
\(b_1=0\)
\(y=2x\)
Rozwiązujemy układ równań obu prostych, otrzymując w ten sposób współrzędne punktu D:
Odległość między dwoma punktami \(A=(x_A,y_A)\) i \(B=(x_B,y_B)\) w układzie współrzędnych wyraża się wzorem:
Korzystamy z powyższego wzoru:
\(C=(1,2), \ D=(-\frac{1}{5},-\frac{2}{5})\)
\(|CD|=h=\sqrt{(1+\frac{1}{5})^2+(2+\frac{2}{5})^2}=\)
\(=\sqrt{(\frac{5}{5}+\frac{1}{5})^2+ (\frac{10}{5}+\frac{2}{5})^2}=\)
\(=\sqrt{(\frac{6}{5})^2+(\frac{12}{5})^2}=\)
\(=\sqrt{\frac{36}{25}+\frac{144}{25}}=\)
\(=\sqrt{\frac{180}{25}}=\sqrt{\frac{36\cdot 5}{25}}=\frac{6\sqrt{5}}{5}\)
Odpowiedź
© medianauka.pl, 2011-01-23, ZAD-1123
Zadania podobne
Zadanie nr 1.
Znaleźć środek ciężkości w trójkącie o wierzchołkach \(A=(-1,0), B=(1,-1)\) i \(C=(1,2)\).
Zadanie nr 2.
Oblicz wysokość w trójkącie równoramiennym o ramionach długości 10 i o podstawie długości 12.
Zadanie nr 3.
W trójkącie równoramiennym o ramionach długości 5 wysokość ma długość 4. Oblicz długość podstawy.
Zadanie nr 4.
W trójkącie prostokątnym jeden z kątów wewnętrznych ma miarę 30°. Oblicz miarę pozostałych kątów w tym trójkącie.
Zadanie nr 5.
W trójkącie \(ABC\) dwa kąty wewnętrzne mają miarę 30°. Długość podstawy jest równa 12. Oblicz długości pozostałych boków trójkąta.
Zadanie nr 6.
W trójkącie \(ABC\) jeden z kątów wewnętrznych ma miarę 30o. Wysokość i bok tego trójkąta, leżące naprzeciwko tego kąta mają długość odpowiednio 3 i 4. Znaleźć długości pozostałych boków tego trójkąta.
Zadanie nr 7.
Czy długość podstawy trójkąta równoramiennego może być dwa razy większa od długości ramienia tego trójkąta?
Zadanie nr 8 — maturalne.
Z odcinków o długościach: \(5, 2a+1, a-1\) można zbudować trójkąt równoramienny. Wynika stąd, że
A. \(a=6\)
B. \(a=4\)
C. \(a=3\)
D. \(a=2\)
Zadanie nr 9 — maturalne.
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o \(50°\). Oblicz kąty tego trójkąta.
Zadanie nr 10 — maturalne.
W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa a oraz \(\angle ABC=\beta\). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac\cdot \cos{\frac{\beta}{2}}}{a+c}\).
Zadanie nr 11.
Korzystając z własności działań na pierwiastkach lub potęgach oblicz: \(\sqrt{2}\cdot \sqrt[4]{4}:\sqrt[5]{16}\).
Zadanie nr 12 — maturalne.
Dany jest czworokąt wypukły \(ABCD\), w którym \(|AD|=|AB|=|BC|=a\), \(|\angle BAD|=60°\) i \(|\angle ADC|=135°\). Oblicz pole czworokąta \(ABCD\).
Zadanie nr 13 — maturalne.
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Na ramieniu AC tego trójkąta wybrano punkt \(M (M\neq A, M\neq C)\), a na ramieniu \(BC\) wybrano punkt \(N\), w taki sposób, że \(|AM| = |CN|\). Przez punkty \(M\) i \(N\) poprowadzono proste prostopadłe do podstawy \(AB\) tego trójkąta, które wyznaczają na niej punkty \(S\) i \(T\). Udowodnij, że \(|ST| = 1/2|AB|\).
Zadanie nr 14 — maturalne.
Prosta \(k\) jest styczna w punkcie \(A\) do okręgu o środku \(O\). Punkt \(B\) leży na tym okręgu i miara kąta \(AOB\) jest równa 80°. Przez punkty \(O\) i \(B\) poprowadzono prostą, która przecina prostą \(k\) w punkcie \(C\) (zobacz rysunek).
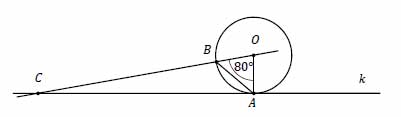
A. 10°
B. 30°
C. 40°
D. 50°