Zadanie - trójkąt równoramienny
Treść zadania:
W trójkącie równoramiennym o ramionach długości 5 wysokość ma długość 4. Oblicz długość podstawy.
Rozwiązanie zadania
Sporządzamy szkic.
Ponieważ mamy do czynienia z trójkątem równoramiennym, wysokość tego trójkąta dzieli go na dwa trójkąty prostokątne. Korzystając z twierdzenia Pitagorasa (suma kwadratów przyprostokątnych trójkąta prostokątnego jest równa kwadratowi przeciwprostokątnej), obliczymy długość podstawy tego trójkąta:
\(4^2+(\frac{1}{2}a)^2=5^2\)
\(16+\frac{a^2}{4}=25\)
\(\frac{a^2}{4}=9/ \cdot 4 \)
\(a^2=36\)
\(a=6\)
Odpowiedź
\(a = 6\)© medianauka.pl, 2011-01-25, ZAD-1127


Zadania podobne
Zadanie nr 1.
Korzystając z własności działań na pierwiastkach lub potęgach oblicz: \(\sqrt{2}\cdot \sqrt[4]{4}:\sqrt[5]{16}\).
Zadanie nr 2.
Dany jest trójkąt o wierzchołkach \(A=(-1,0), B=(1,-1)\) i \(C=(1,2)\). Oblicz długość wysokości tego trójkąta opuszczonej z wierzchołka C.
Zadanie nr 3.
Znaleźć środek ciężkości w trójkącie o wierzchołkach \(A=(-1,0), B=(1,-1)\) i \(C=(1,2)\).
Zadanie nr 4.
Oblicz wysokość w trójkącie równoramiennym o ramionach długości 10 i o podstawie długości 12.
Zadanie nr 5.
W trójkącie prostokątnym jeden z kątów wewnętrznych ma miarę 30°. Oblicz miarę pozostałych kątów w tym trójkącie.
Zadanie nr 6.
W trójkącie \(ABC\) dwa kąty wewnętrzne mają miarę 30°. Długość podstawy jest równa 12. Oblicz długości pozostałych boków trójkąta.
Zadanie nr 7.
W trójkącie \(ABC\) jeden z kątów wewnętrznych ma miarę 30o. Wysokość i bok tego trójkąta, leżące naprzeciwko tego kąta mają długość odpowiednio 3 i 4. Znaleźć długości pozostałych boków tego trójkąta.
Zadanie nr 8.
Czy długość podstawy trójkąta równoramiennego może być dwa razy większa od długości ramienia tego trójkąta?

Zadanie nr 9 — maturalne.
Z odcinków o długościach: \(5, 2a+1, a-1\) można zbudować trójkąt równoramienny. Wynika stąd, że
A. \(a=6\)
B. \(a=4\)
C. \(a=3\)
D. \(a=2\)

Zadanie nr 10 — maturalne.
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o \(50°\). Oblicz kąty tego trójkąta.

Zadanie nr 11 — maturalne.
W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa a oraz \(\angle ABC=\beta\). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac\cdot \cos{\frac{\beta}{2}}}{a+c}\).

Zadanie nr 12 — maturalne.
Dany jest czworokąt wypukły \(ABCD\), w którym \(|AD|=|AB|=|BC|=a\), \(|\angle BAD|=60°\) i \(|\angle ADC|=135°\). Oblicz pole czworokąta \(ABCD\).

Zadanie nr 13 — maturalne.
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Na ramieniu AC tego trójkąta wybrano punkt \(M (M\neq A, M\neq C)\), a na ramieniu \(BC\) wybrano punkt \(N\), w taki sposób, że \(|AM| = |CN|\). Przez punkty \(M\) i \(N\) poprowadzono proste prostopadłe do podstawy \(AB\) tego trójkąta, które wyznaczają na niej punkty \(S\) i \(T\). Udowodnij, że \(|ST| = 1/2|AB|\).

Zadanie nr 14 — maturalne.
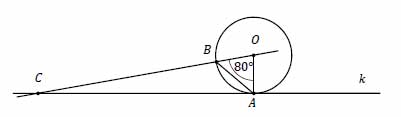
Prosta \(k\) jest styczna w punkcie \(A\) do okręgu o środku \(O\). Punkt \(B\) leży na tym okręgu i miara kąta \(AOB\) jest równa 80°. Przez punkty \(O\) i \(B\) poprowadzono prostą, która przecina prostą \(k\) w punkcie \(C\) (zobacz rysunek).
A. 10°
B. 30°
C. 40°
D. 50°

