Zadanie - wzajemne położenie prostych na płaszczyźnie
Treść zadania:
Znaleźć równania wszystkich prostych prostopadłych przechodzących przez punkty \(A(1,2), B(2,-1), C(-1,3)\).
 Rozwiązanie zadania
Rozwiązanie zadania
Sporządzamy rysunek:
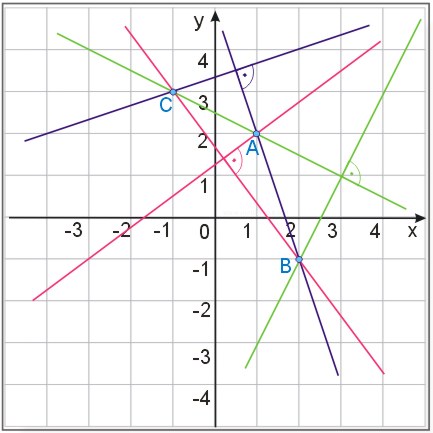
Mamy aż trzy różne przypadki oznaczone na rysunku różnymi kolorami. Rysunek sporządzamy następująco: przez dowolne dwa punkty prowadzimy prostą, a następnie przez trzeci punkt prowadzimy prostą prostopadłą. Musimy znaleźć równania wszystkich prostych.
1) Proste oznaczone kolorem granatowym.
Wiemy, że jedna z prostych przechodzi przez punkty \(A\) i \(B\). Podstawiamy zatem ich współrzędne do ogólnego równania prostej \(y=ax+b\), aby wyznaczyć współczynniki \(a\) oraz \(b\).
\(A(1,2), B(2,-1)\)
\(y=ax+b\)
\(\begin{cases}2=a\cdot 1+b\\ -1=a\cdot 2+b\end{cases}\)
\(\underline{_-\begin{cases}2=a+b\\ -1=2a+b\end{cases}}\)
\(2-(-1)=a-2a\)
\(3=-a/:(-1)\)
\(a=-3\)
\(2=a+b\)
\(2=-3+b\)
\(b=5\)
\(y=-3x+5\)
Teraz wystarczy skorzystać z własności położenia prostych na płaszczyźnie, pamiętając że proste równoległe mają równe współczynniki kierunkowe prostych, a proste prostopadłe mają współczynniki kierunkowe spełniające warunek:
Znajdziemy teraz prostą prostopadłą do \(y=-3x+5\), która przechodzi przez punkt \(C(-1,3)\). Oznaczmy równanie szukanej prostej przez \(y=a_1x+b_1\). Współczynniki kierunkowe obu prostych muszą być przeciwne i odwrotne, a więc są równe liczbie \(\frac{1}{3}\). Wystarczy teraz podstawić współrzędne punktu C do równania szukanej prostej i w ten sposób wyznaczymy współczynnik \(b_1\):
\(y=a_1x+b_1\)
\(a_1=-\frac{1}{-3}=\frac{1}{3}\)
\(y=\frac{1}{3}x+b_1\)
\(C(-1,3)\\ 3=\frac{1}{3}\cdot (-1)+b_1\)
\(-b_1=-3\frac{1}{3}/:(-1)\)
\(b_1=3\frac{1}{3}\)
\(\underline{y=\frac{1}{3}x+3\frac{1}{3}}\)
Z pozostałymi przypadkami postępujemy identycznie jak wyżej. Będziemy stosować te same oznaczenia współczynników niezależnie od przyjętych w przypadku pierwszym.
2) Proste oznaczone kolorem różowym.
Wiemy, że jedna z prostych przechodzi przez punkty \(B\) i \(C\). Podstawiamy zatem ich współrzędne do ogólnego równania prostej \(y=ax+b\), aby wyznaczyć współczynniki \(a\) oraz \(b\).
\(B(2,-1), C(-1,3)\)
\(y=ax+b\)
\(\begin{cases}-1=a\cdot 2+b\\ 3=a\cdot (-1)+b\end{cases}\)
\(\underline{_-\begin{cases}-1=2a+b\\ 3=-a+b\end{cases}}\)
\(-1-3=2a-(-a)\)
\(-4=3a/:3\)
\(a=-\frac{4}{3}\)
\(3=-a+b\)
\(3=-(-\frac{4}{3})+b\)
\(b=3-1\frac{1}{3}\)
\(b=1\frac{2}{3}\)
\(\underline{y=-\frac{4}{3}x+1\frac{2}{3}}\)
Teraz wystarczy skorzystać z własności położenia prostych na płaszczyźnie, pamiętając że proste równoległe mają równe współczynniki kierunkowe prostych, a proste prostopadłe mają współczynniki kierunkowe spełniające warunek:
Znajdziemy teraz prostą prostopadłą do wyżej wyznaczonej, która przechodzi przez punkt \(A(1,2)\). Oznaczmy równanie szukanej prostej przez \(y=a_1x+b_1\). Współczynniki kierunkowe obu prostych muszą być przeciwne i odwrotne. Wystarczy teraz podstawić współrzędne punktu \(A\) do równania szukanej prostej i w ten sposób wyznaczymy współczynnik \(b_1\):
\(y=a_1x+b_1\)
\(a_1=-\frac{1}{-\frac{4}{3}}=\frac{3}{4}\)
\(y=\frac{3}{4}x+b_1\)
\(A(1,2)\\ 2=\frac{3}{4}\cdot 1+b_1\)
\(-b_1=-2+\frac{3}{4}/:(-1)\)
\(b_1=1\frac{1}{4}\)
\(\underline{y=\frac{3}{4}x+1\frac{1}{4}}\)
3) Proste oznaczone kolorem zielonym.
Wiemy, że jedna z prostych przechodzi przez punkty \(A\) i \(C\). Podstawiamy zatem ich współrzędne do ogólnego równania prostej (\(y=ax+b\)), aby wyznaczyć współczynniki \(a\) oraz \(b\).
\(A(1,2), C(-1,3)\)
\(y=ax+b\)
\(\begin{cases}2=a\cdot 1+b\\ 3=a\cdot (-1)+b\end{cases}\)
\(\underline{_-\begin{cases}2=a+b\\ 3=-a+b\end{cases}}\)
\(2-3=a-(-a)\)
\(-1=2a/:2\\a=-\frac{1}{2}\)
\(3=-a+b\)
\(3=-(-\frac{1}{2})+b\)
\(b=3-\frac{1}{2}\)
\(b=2\frac{1}{2}\)
\(\underline{y=-\frac{1}{2}x+2\frac{1}{2}}\)
Teraz wystarczy skorzystać z własności położenia prostych na płaszczyźnie, pamiętając że proste równoległe mają równe współczynniki kierunkowe prostych, a proste prostopadłe mają współczynniki kierunkowe spełniające warunek:
Znajdziemy teraz prostą prostopadłą do wyżej wyznaczonej, która przechodzi przez punkt \(B(2,-1)\). Oznaczmy równanie szukanej prostej przez \(y=a_1x+b_1\). Współczynniki kierunkowe obu prostych muszą być przeciwne i odwrotne. Wystarczy teraz podstawić współrzędne punktu B do równania szukanej prostej i w ten sposób wyznaczymy współczynnik \(b_1\):
\(y=a_1x+b_1\)
\(a_1=-\frac{1}{-\frac{1}{2}}=2\)
\(y=2x+b_1\)
\(B(2,-1)\)
\(-1=2\cdot 2+b_1\)
\(-b_1=4+1/:(-1)\)
\(b_1=-5\)
\(\underline{y=2x-5}\)
© medianauka.pl, 2010-03-12, ZAD-687


Zadania podobne
Zadanie nr 1.
Dana jest prosta o równaniu \(y=-7x+5\). Znaleźć równanie prostej równoległej do tej prostej, przechodzącej przez początek układu współrzędnych.
Zadanie nr 2.
Dana jest prosta o równaniu \(y=5x+\frac{1}{5}\). Znaleźć równanie prostej prostopadłej do tej prostej, przechodzącej przez punkt \(A(1,-1)\).
Zadanie nr 3.
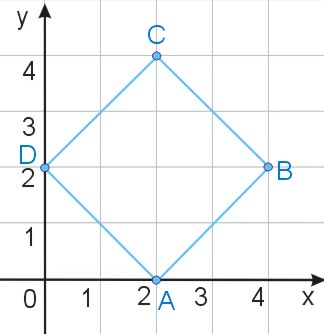
Znaleźć równania prostych zawierających boki kwadratu ABCD, jeśli wiadomo, że współrzędne wierzchołków są liczbami całkowitymi.
Zadanie nr 4.
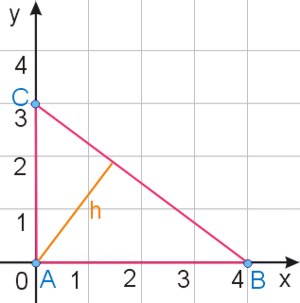
Znaleźć równanie prostej, która zawiera wysokość w trójkącie \(ABC\) przedstawionym na poniższym rysunku:

Zadanie nr 5 — maturalne.
Proste opisane równaniami \(y=\frac{2}{m-1}x+m-2\) oraz \(y=mx+\frac{1}{m+1}\) są prostopadłe, gdy:
A. \(m=2\)
B. \(m=\frac{1}{2}\)
C. \(m=\frac{1}{3}\)
D. \(m=-2\)

Zadanie nr 6 — maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.

Zadanie nr 7 — maturalne.
Prosta l o równaniu \(y=m^2x+3\) jest równoległa do prostej k o równaniu \(y=(4m-4)x-3\). Zatem:
A. \(m=2\)
B. \(m=-2\)
C. \(m=-2-2\sqrt{2}\)
D. \(m=-2+2\sqrt{2}\)

Zadanie nr 8 — maturalne.
Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla:
A. \(m=-\frac{1}{2}\)
B. \(m=\frac{1}{2}\)
C. \(m=1\)
D. \(m=2\)

Zadanie nr 9 — maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)

Zadanie nr 10 — maturalne.
W układzie współrzędnych punkty \(A=(4,3)\) i \(B=(10,5)\) są wierzchołkami trójkąta ABC. Wierzchołek \(C\) leży na prostej o równaniu \(y=2x+3\). Oblicz współrzędne punktu \(C\), dla którego kąt \(ABC\) jest prosty.

Zadanie nr 11 — maturalne.
Proste o równaniach \(y=(2m+2)x−2019\) oraz \(y=(3m−3)x+2019\) są równoległe, gdy
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=5\)

Zadanie nr 12 — maturalne.
Prosta o równaniu \(y=ax+b\) jest prostopadła do prostej o równaniu \(y=− 4x+1\) i przechodzi przez punkt \(P=(\frac{1}{2},0)\), gdy
A. \(a=-4\) i \(b=-2\)
B. \(a=\frac{1}{4}\) i \(b=-\frac{1}{8}\)
C. \(a=-4\) i \(b=2\)
D. \(a=\frac{1}{4}\) i \(b=\frac{1}{2}\)

Zadanie nr 13 — maturalne.
Proste o równaniach \(y=(m−2)x\) oraz \(y=\frac{3}{4}x+7\) są równoległe. Wtedy
A. \(m=-\frac{5}{4}\)
B. \(m=\frac{2}{3}\)
C. \(m=\frac{11}{4}\)
D. \(m=\frac{10}{3}\)

Zadanie nr 14 — maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
Proste o równaniach \(y=3x-5\) oraz \(y=\frac{(m-3)}{2}+\frac{9}{2}\) są równoległe, gdy
A. \(m=1\)
B. \(m=3\)
C. \(m=6\)
D. \(m=9\)

Zadanie nr 15 — maturalne.
Dane są cztery proste k, l, m o równaniach:
\(k: y=-x+1\)
\(l: y=\frac{2}{3}x+1\)
\(m: y=-\frac{3}{2}x+4\)
\(n: y=-\frac{2}{3}x-1\)
Wśród tych prostych prostopadłe są
A. proste k oraz l.
B. proste k oraz n.
C. proste l oraz m.
D. proste m oraz n.

Zadanie nr 16 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) dana jest prosta \(k\) o równaniu \(y=-\frac{1}{3}x+2\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Prosta o równaniu \(y=ax+b\) jest równoległa do prostej \(k\) i przechodzi przez punkt \(P=(3,5)\), gdy
A. \(a=3, b=4\)
B. \(a=-\frac{1}{3}, b=4\)
C. \(a=3, b=-4\)
D. \(a=-\frac{1}{3}, b=6\)

